Проектирование алгоритма управления электрогидравлическим приводом», страница 2

Объект регулирования, в трактовке схемы рис.1, в электрогидравлическом следящем приводе состоит из ЭМП, золотникового механизма и управляемого им гидроцилиндра, шток которого жестко связан с перемещаемым инерционным объектом, и датчика положения. Математическое описание объекта регулирования состоит из уравнений его элементов, записанных на основании физических законов, характеризующих их функционирование, а также из уравнений связи. В совокупности они образуют систему уравнений объекта.

Электромеханический преобразователь в самом грубом приближении описывается уравнением:

h=КэмпUp (1.1)

Такое упрощенное описание предполагает, что ЭМП является безынерционным элементом и не вносит запаздывания. Это допущение, строго говоря, справедливо только для приводов малой мощности.

Сколько-нибудь строгое математическое описание золотникового механизма и управляемого им гидроцилиндра представляет собой систему нелинейных дифференциальных уравнений. Для выполнения анализа в первом приближении эту систему линеаризуют методом малых отклонений. Такая линеаризация заключается в разложении нелинейных функций в ряд Тейлора в окрестности некоторого номинального режима с удержанием только линейных членов. В данном конкретном случае за номинальный принимают режим, когда   h=h°=0 (среднее положение золотника), y=y°=0 (среднее положение поршня) и P=P1-P2=0, P1 и P2 - давления в верхней и нижней полости цилиндра. Т.е. за номинальные приняты средние значения диапазона изменения переменных. При этом отклонения от номинальных значений совпадает с самими переменными: Dh=h-h°=h и т.д.

Первое из давлений, описывающих систему “золотник - цилиндр” называется уравнением расхода и является математическим отображением условия неразрывности потока жидкости:

Qз = Qц

Qз - подача жидкости через золотниковый механизм;

Qц - расход жидкости в гидроцилиндре.

В линеаризованной форме

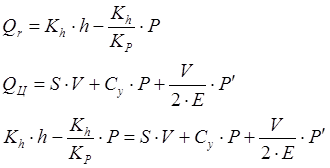      (1.2)

Физический смысл слагаемых уравнения (1.2.) следующий:

Первое слагаемое левой части - это подача идеального золотникового механизма на холостом ходу, т.е. при отсутствии перепада давления в гидроцилиндре. Второе слагаемое левой части показывает уменьшение подачи золотника при появлении перепада давления в цилиндре. Оно возникает из-за перепада давления на золотниковых щелях. Первое слагаемое правой части - “полезный” расход, обеспечивающий движение поршня. Второе слагаемое - расход перетечек жидкости из полости высокого в полость низкого давления, неизбежный во всяком реальном гидродвигателе. Наконец, третье слагаемое правой части - это так называемый компрессорный расход: изменение объема жидкости при изменении давления, являющееся следствием довольно значительной ее сжимаемости.

Второе уравнение, описывающее систему “золотник - цилиндр” называется уравнением давлений. По сути это уравнение баланса сил на штоке гидроцилиндра. В линейной форме оно имеет вид:

Sn·P= m·V¢+ fV + Fвн  (1.3.)

m -масса всех подвижных частей, связанных со штоком;

f - коэффициент вязкого трения;

Fвн - внешнее возмущающее усилие, в общем случае являющееся случайной функцией времени.

Датчик положения будет считать безынерционным, и его выход отождествлять с положением нагрузки y.