Проектирование алгоритма управления электрогидравлическим приводом», страница 8

В системе стабилизации ошибка формируется как разность между постоянной установкой, соответствующей заданному значению температуры, и выходом датчика температуры. Установка может хранится в памяти машины, либо приходить в один из портов ЭВМ более высокого иерархического уровня.

Сформированный ЭВМ в соответствии с алгоритмом (4.3) сигнал управления должен быть выдан в один из портов для последующего цифро-аналогового преобразования.

1III     Выполнение работы

по индивидуальным данным

2III.1 Исходные данные

Данные объекта             Требования к системе

E	=	109        Па	tp	=	0,15     c
hо	=	0,95    -	qдоп	=	5*10-3    м
r	=	900     кг/м3	Ag	=	0,2        м
s	=	30*10-6  м	wg	=	5        c-1
D	=	0,04    м	Fвн	=	1*103         Н
Рн	=	6       MПа
L	=	0,2     м
m	=	0,5*103 кг
hmax	=	0.001   м
b	=	0,03    м
m	=	0,7     -
Kш	=	0.4-0.6 -

2III.2 МаТематическое описание системы

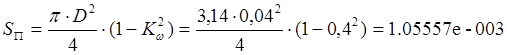
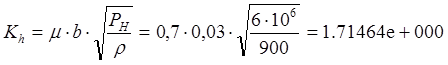
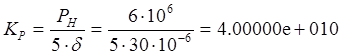
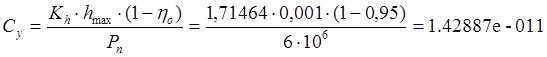
V @ 0,6*S_П*L = 0,6*0,00105557*0,2 = 1.266690e-004

Матрицы уравнения состояния системы:

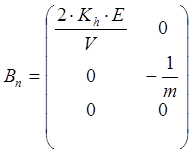
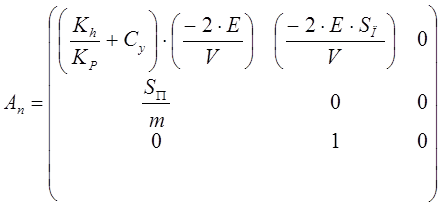
С= (0   0   1)

D= (0   0)

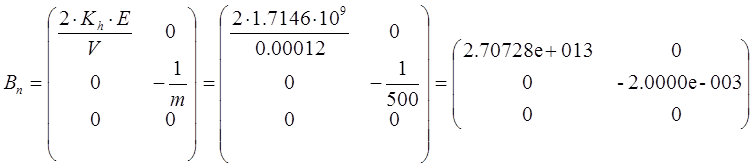
С= (0   0   1)

D= (0   0)

Произведем выбор периода квантования системы:

c.

Далее, находим полюса передаточной функции непрерывной части, что делается с помощью функции MATLAB SS2ZP:

[z,p,k]=ss2zp(An,Bn_,Cn,Dn,1)

Вектор Рн составлен из полюсов передаточной функции непрерывной части.

0

p =   -4.083833156234613e+001

-8.615885217173716e+002

Дискретная модель объекта может быть задана в форме системы разностных уравнений состояния: X(k+1)=AX(k)+BU(k). Матрицы А и В могут быть определены с помощью функции C2D:

[Ad,Bd]=c2d(A, B, То)

3.514647016430293e-002   -1.643374807358630e+007   0

Ad= 2.081646694267021e-009    9.249601075440594e-001   0

4.502393548497771e-012    2.910602763701082e-003   1

2.669446001057125e+010    7.108910605044431e+001

Bd= 1.218924252659323e+002   -5.821205527402160e-006

1.452140400082277e-001   -8.850959103963462e-009

Передаточные функции находятся для каждого входа отдельно с помощью функции SS2TF: [N_iV,D_iV]=ss2tf(Ad,Bd,C,D,iv), где iv - номер входа.

Для 1-го входа:

N1 =   0    1.45214e-001    3.35548e-001    3.87678e-002

D1 =   1   -1.96010e+000    1.02682e+000   -6.67183e-002

Для 2-го входа:

N2 =   0   -8.85095e-009   -8.12528e-009    5.70355e-010

D2 =   1   -1.96010e+000    1.02682e+000   -6.67183e-002

2III.3 Анализ системы

при использовании пропорционального регулятора

Пропорциональный регулятор является простейшим из возможных. Алгоритм управления имеет вид:

Up=-KpYu

Кр - постоянный коэффициент,

Yu- измеряемая координата.

Для электрогидравлического привода Yu=y,

Величину Кр будем определять подбором, для чего воспользуемся функцией RLOCUS, которая ищет корни характеристического уравнения 1+kpWu=0

Обращение к функции имеет вид R=RLOCUS(N,D,К),

N и D - векторы коэффициентов числителя и знаменателя передаточной функции Wu, а К - вектор значений коэффициентов Кр, при которых ищутся корни характеристического уравнения.

В нашем случае:

k=0,001:0.01:0.25

r=rlocus(N1,D1,k)

...

...

9.3549e-001+ 3.2617e-001i 9.3549e-001- 3.2617e-001i 6.0074e-002              

9.3511e-001+ 3.3433e-001i 9.3511e-001- 3.3433e-001i 5.9396e-002             

9.3472e-001+ 3.4229e-001i 9.3472e-001- 3.4229e-001i 5.8726e-002             

r=        9.3432e-001+ 3.5006e-001i 9.3432e-001- 3.5006e-001i 5.8063e-002