Информатика и выч. техника \ Проектированию компьютерных систем управления

Проектирование алгоритма управления электрогидравлическим приводом», страница 7

-форма ЖЛЧХ, особенно в высокочастотной части, должна по возможности повторять форму ЛЧХ передаточной функции Wu(jl). Наклоны высокочастотных асимптот должны совпадать обязательно. 

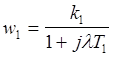
По построенному графику амплитудной ЖЛЧХ необходимо восстановить передаточную функцию Wu(jl). Переход от амплитудной характеристики к передаточной функции вообще говоря неоднозначен. Например, передаточные функции  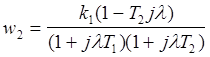и  имеют одинаковые амплитудные ЛЧХ.

Обязательно выполнение следующего правила: передаточная функция Wж(jl) должна иметь те же номинальнофазовые нули, т.е. те же сомножители числителя, в которых есть отрицательные слагаемые, которые имеются в передаточной функции Wu(jl). Несоблюдение этого условия приводит к практической неработоспособности системы.

После того, как передаточная функция Wж(jl) получена, передаточная функция Wk(jl), соответствующая алгоритму управления, находится простым делением

Если в числителе и в знаменателе Wk(jl) окажутся сомножители с постоянными времени, отличающимися не более чем на 20 %, их допустимо сократить.

Переход от Wk(jl) к функции Wk(z) осуществляется с помощью функции MATLAB Z2W

[D,N]=Z2W(DW,NW,T0).

Здесь D, N- векторы коэффициентов полиномов знаменателя и числителя W(z), а DW, NW -соответствующие векторы W(jl) (по убыванию степени) Векторы D и N вычисляются с точностью до одного постоянного множителя, который следует сократить.

Метод ЛЧХ является приближенным, поэтому необходимо проверить качество переходного процесса и точность системы, достигаемую при алгоритме управления, описываемом функцией Wk(z). Эта проверка подробно рассмотрена в п.3. В формуле (3.4) и всех последующих необходимо произведение КрWu(jl) заменить на произведение Wk(z)* Wu(z)= W(z). В остальном рассчет не отличается от описанного. Графики должны быть представлены в записке. До начала расчета необходимо сократить общие множители числителя и знаменателя W(z), если они имеются.

Для следящей системы, кроме того, необходимо оценить установившуюся ошибку от постоянного возмущающего воздействия. Для этого необходимо сформировать функцию

FФF(z)=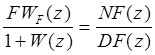

где F- значение возмущающего воздействия из задания, а затем воспользоваться функцией DSTEP.

Если проверка дала удовлетворительные результаты, можно переходить к реализации алгоритма управления, для чего необходимо записать этот алгоритм в явной форме. Ресурсы управляющей ЭВМ используются наиболее рационально, если коэффициент передачи функции Wk близок к единице. Для выполнения этого условия в аналоговой части системы вводят дополнительные усилительные элементы с коэффициентом Кдоп (вопросы реализации не рассматриваются), а в ЭВМ реализуют алгоритм, соответствующий функции 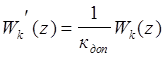. Для электромеханической следящей системы  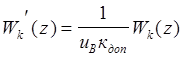объяснение этому дано ниже.Передаточную функцию Wu’ нужно представить в форме

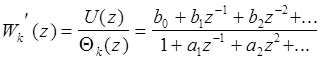
Отсюда U(z)+a1U(z)z+a2U(z)z2+...= b0q(z)+b1q(z)z-1+b2q(z)z-2+...

и U(z)=b0q(z)+b1q(z)z-1+...- a1U(z)z-1-a2U(z)z2...

Поскольку домножение z-изображения решетчатой функции на z-n соответствует ее сдвигу на n тактов квантования, из последнего выражения непосредственно получается алгоритм

U(k)=b0q(k)+b1q(k-1)+...- a1U(k-1)-a2U(k-2)...                                      (4.3)

Сигнал ошибки в различных системах формируется различным образом , в связи с чем возникают особенности в реализации алгоритма.

В электрогидравлической следящей системе этот сигнал (q=yg-y) должен быть сформирован в управляющей ЭВМ. Предполагается, что в один из портов ЭВМ подается код, соответствующий управляющему сигналу yg, а другой порт принимает сигнал y от цифрового датчика положения.

В электромеханической следящей системе сигнал от чувствительного элемента, равный UB*q поступает через АЦП в один из портов ЭВМ. Коэффициент UB необходимо учесть, для чего перед получением алгоритма на него следует поделить полученную функцию Wu(jl).      

Скачать файл