Проектирование алгоритма управления электрогидравлическим приводом», страница 3

Таким образом, объект регулирования описывается уравнениями(1.1.)¸(1.3.)и кинематическим соотношением y¢=V

Целесообразно объединить уравнения (1.1.) и (1.2.) и получить математическое описание объекта в виде системы дифференциальных уравнений первого порядка:

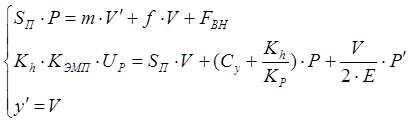     (1.4)

Для дальнейших преобразований систему (1.4.) необходимо привести к канонической форме уравнений состояния. Объект имеет два входных воздействия - управляющее Up и возмущающее Fвн - которые должны составить вектор - столбец входных сигналов U. Координаты объекта - давление P, скорость V и перемещение y -составят вектор координат X. Выход объекта Y совпадает с соответствующей координатой. Переход от (1.4.) к системе уравнений состояния вида

X¢=AnX + BnU          (1.5.)

y= Cx+Du             (1.6.)

    

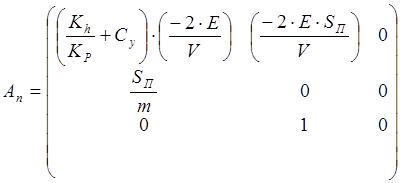
C_п = (0 0 1);   D_п = (0 0)

Численные значения коэффициентов уравнений (1.1.)¸(1.3.) частично приведены в задании на проектирование. Другие могут быть рассчитаны в соответствии с приведенными ниже указаниями. Коэффициент Кэмп, как уже было сказано, можно на первом этапе принять равным единице.

Крутизна расходной характеристики Kh определяется по формуле . Ширина щели b и давление питания Рn заданы. Коэффициент расхода m =0,7 , плотность рабочей жидкости r@900 кг/м³ .

Крутизну силовой характеристики находят по полуэмпирической формуле 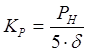. Здесь d - радиальный зазор в золотниковой паре, d = 5 ¸ 25 мкм.

Эффективная площадь поршня рассчитывается по очевидной формуле: 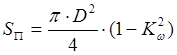, где Кш = dш/Dn - отношение диаметра штока к диаметру поршня, Кш =0,4¸ 0,6.

Коэффициент утечек находят исходя из объемного КПД h_о=0,96¸0,98, давления питания P_n и номинальной  подачи Q_н. Последнюю можно определить из  выражения  Q_н = K_h·h_max, где h_max - максимальное смещение золотника. Расчетная формула для коэффициента утечек: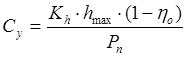

Объем  жидкости  в  полости цилиндра вычисляется ориентировочно : V@0,6·S_n·L,  L - полный ход поршня.

Значение модуля объемной упругости E@ 10⁹ Н/м².

1II Выбор периода квантования и построениедискретноймодели объекта регулирования

При использовании цифровой коррекции к объекту регулирования, кроме непрерывной неизменяемой части, относят также цифроаналоговый преобразователь, модель которого представляют в виде идеального импульсного элемента и фиксатора нулевого порядка. Условно считается, что измерение выходных координат происходит только в моменты времени, кратные периоду квантования Т_о. Схема объекта регулирования в цифровой системе может быть представлено в виде рис.2.1

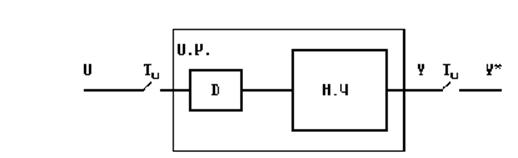
Рис.3

На рисунке 3 обозначено: Ф- фиксатор нулевого порядка, Н.Ч- непрерывная часть (объект), математическое описание которого получено в предыдущем разделе.

Период квантования Т_о может быть либо задан исходя из возможностей ЭВМ, либо рассчитан на основании требований к длительности переходного процесса t_р. Для расчета используется неравенство То<tp/(1-2)P, которое рекомендуется выполнять с запасом в 4-10 раз.

Кроме того, к нежелательным эффектам может привести близость периода квантования к постоянным времени колебательных звеньев непрерывной части (если таковые имеются). Необходимо найти полюса передаточной функции непрерывной части, что делается с помощью функции MATLAB

[Z_н,P_н,K_н]=SS2ZP(A_н,B_н,C,D,iv)

Здесь A_н,B_н,C,D- матрицы из системы (5)(6), iv- номер входа управляющего воздействия.

Вектор Р_н будет составлен из полюсов передаточной функции непрерывной части. При наличии колебательного звена вектор Р_н содержит пару комплексно-сопряженных полюсов - α+jβ. Постоянная времени колебательного звена Т_к находится по формуле

_-1/2

Тк=( α ²+β²)

Вектор Р_н не должен иметь составляющих с положительной вещественной частью. Их наличие говорит об ошибке в расчетах.

Дискретная модель объекта может быть задана в форме системы разностных уравнений состояния

X(k+1)=AX(k)+BU(k)                       (2.1)

y(k)=CX(k)+DU(k),                        (2.2)

где X(k),y(k),U(k)-  дискретные  аналоги  непрерывных  переменных   из (1.5), (1.6).