Проектирование алгоритма управления электрогидравлическим приводом», страница 4

Матрицы А и В связаны с матрицами А_н, В_н непрерывной модели соотношениями

А=ехрА_нТ_{о                 То}

В=Вн∫ ехрАн t dt

                              ⁰

Определяются эти матрицы с помощью функции MATLAB  [А,В]=С2d(А_н,В_н,Т_о).

Другой способ задания дискретной модели- описание объекта с помощью передаточных функций с использованием z-преобразования.

В следящей системе объект регулирования имеет единственную выходную величину y (перемещение или угол поворота инерционного объекта) и два входных воздействия i (компоненты вектора U)- управление (U_р) и возмущение (M_пр или F_вн). Он будет полностью описываться двумя передаточными функциями

Y(z)              Y(z)             Y(z)

W_U(z)=-----       W_F(z)=-----      W_M(z)=----U_p(z)             F(z)              M(z)

Его структурная схема имеет вид, рис.4

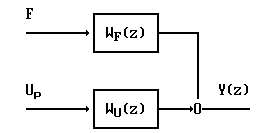
Рис.4

Каждую из этих передаточных функций можно представить в форме отношения полиномов

N(z)   b_nzⁿ+^...+b₁z+b_o

W(z) _{= ----- = -------------------------------}               (2.3)

D(z)   a_nzⁿ+^...+a₁z+a_o

либо в виде отношения произведений элементарных сомножителей

(z-z₁)(z-z₂)^...(z-z_n)

W(z) = K---------------------            (2.4)

(z-p₁)(z-p₂)^...(z-p_n)
1III   Анализ возможностей системы при

использовании пропорционального регулятора.

Пропорциональный регулятор является простейшим из возможных.  Алгоритм управления имеет вид:

U_р=-К_рy_u, где у_р- постоянный  коэффициент,  а  y_u -  измеряемая  координата.  Для электрогидравлического привода y_u=y,  для электромеханического привода у=U_Ву, а для системы стабилизации y_u=y₁. В динамических расчетах можно условно положить U_b=1,  а реальное значение этого коэффициента (обычно U_b=30-110 В) необходимо будет учесть на последнем этапе проектирования при реализации алгоритма управления.  Структурная схема системы с пропорциональным регулятором имеет вид рис.5.

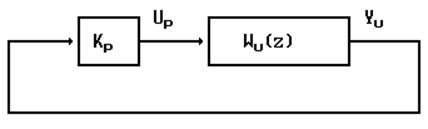
Рис.5

Значение коэффициента К_р должно удовлетворять условиям замкнутой системы:

К_р < K_кр

где Ккр то значение Кр, при котором система теряет устойчивость. В некоторых случаях неравенство может оказаться двусторонним:

К_кр1 < К_р < К_кр2

Величину Кр можно выбрать либо аналитически, определяя Ккр по критериям устойчивости, либо определить подбором.

Простейший способ аналитического определения значения К_кр состоит в следующем. В передаточной функции W_u(z) переходят к w-преобразованию. Это делается с использованием функции MATLAB-CTRL W2Z, обращение к которой имеет вид:

[DW,NW]= W2Z(D,N,T_o)

Здесь D и N- векторы коэффициентов полиномов знаменателя и числителя передаточной функции W_u(z), расположенных по убыванию степени z, а Т_о- период квантования. Результатом операции будут векторы коэффициентов полиномов DW и NW знаменателя и числителя передаточной функции

NW(w)

W_u(w)=--------DW(w)

Характеристическое уравнение системы имеет вид 1+K_pW_u(w)=0, или в развернутой форме

DW(w)+K_pNW(w)=0   (3.1)

Поскольку во всех рассматриваемых случаях объект описывается передаточными функциями третьего порядка, приводя в (3.1) подобные, можно представить характеристическое уравнение в форме

a₃(К_p)w³+a₂(К_p)w²+a₁(К_p)w+a₀(К_p)=0

Согласно критерию Гурвица, условие устойчивости системы записывается в форме а₁а₂>а₀а₃ и, следовательно, значение К_кр находится из уравнения

a₁(К_кр)a₂(К_кр)=a₀(К_кр)a₃(К_кр)    (3.2)

После решения этого уравнения, величину К_кр выбирают равной К_р=(0.7-0.9)К_кр с целью обеспечения некоторого запаса устойчивости.

Если исполнитель хочет избежать аналитических расчетов, связанных с решением (3.2), то приемлемое значение К_р можно найти подбором. Это делается с помощью функции MATLAB-CTRL RLOCUS, которая ищет корни характеристического уравнения

1+k_pW_u=0 (3.2)

Обращение к функции имеет вид               R=RLOCUS(N,D,K),   где N и D- векторы коэффициентов числителя и знаменателя  передаточной функции W_u,  а K- вектор значений коэффициентов К_р, при которых ищутся корни характеристического уравнения. Он обычно формируется в виде:

К=К_{р нач} Δ: K_р:К_{р кон}