Проектирование алгоритма управления электрогидравлическим приводом», страница 6

рис 4.1

 

На рис 4.1 через W_к(z) обозначена передаточная функция, описывающая алгоритм управления , которую надлежит определить.

Идея метода логарифмических частотных характеристик (ЛЧХ) состоит в приведении передаточной функции разомкнутой системы W(z)=W_k(z)*W_u(z) к виду некой желаемой передаточной функции W_ж(z), т.е. в обеспечении условия W(z)=W_ж(z). Желаемая передаточная функция выбирается исходя из требований к системе. Расчеты выполняются графоаналитическим методом с использованием логарифмических характеристик, построенных в функции псевдочастоты l. Для получения характеристик известной передаточной функции, например W_u(z), необходимо перейти от z-преобразования к w-преобразованию, а затем сделать замену w=jl. Этот переход выполняется с помощью функции W2Z (см п. 3), в результате применения которой находится передаточная функция

W_u(jl)=

Для построения логарифмической переходной характеристики необходимо представить функцию W_u(jl) в форме отклонения произведений типовых звеньев, что достигается использованием функции

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Эта функция дает представление  W_u(jl) в виде

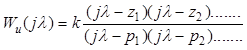
Переход к форме типовых звеньев

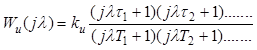     (4.1)

очевиден t_i=; T_i=; k_u=k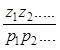

Паре комплексно-сопряженных корней числителя или знаменателя, например z_1,2=-a±jb соответствует сомножитель вида

t²(jl)²+2Vtjl+1

причем

t=

Построение логарифмических частотных характеристик (ЛЧХ) функции (4.1) производится точно так же, как для непрерывных систем.

Желаемая передаточная функция W_ж(jl) находится в противоположном порядке: сначала по определенным правилам строится график ЛЧХ, соответствующий W_ж(jl) (так называемая ЖЛЧХ), а затем по этому графику восстанавливается передаточная функция.

Низкочастотная часть ЖЛЧХ строится на основании требований к точности системы в установившемся режиме. Для следящей системы основной причиной возникновения ошибки в установившемся режиме работы является изменение задающего  y_g(t) или a_g(t). Для системы стабилизации основной источник ошибки - возмущающее воздействие DQ и Dt. В задании на проектирование то и другое воздействие полагается синусоидальным.

)

DQ=a_bsinw_bt, (Dt=a_bsinw_bt)

Мерой точности системы является амплитуда установившейся ошибки q_m , величина которой задана. Значение амплитуды ошибки для следящей системы рассчитывается по формуле.

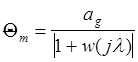   l=w₃

Если пренебречь единицей в знаменателе этих формул (что допустимо практически всегда), то можно получить следующие требования к желаемой передаточной функции: для следящей системы  ½w_ж(jw₃)½³

Это означает, что ЖЛЧХ должна проходить выше критической точки с абсциссой lgw_b и ординатой 20lgдля следящей системы либо   20lg½w_Q(jw_b)½ . Формально это единственное требование к низкочастотной части ЖЛЧХ.

Среднечастотная часть ЖЛЧХ  формируется на основании требований к переходным процессам  в системе, причем учитываются два основных показателя : длительность переходного процесса (время регулирования) t_p и перерегулирования s. Заданное время регулирования обеспечивается выполнением неравенства

l_с - частота среза ЖЛЧХ.

Большие значения множителя в числителе (4.2) следует выбирать при более колебательных переходных процессах.

Требования к перерегулированию в задании на проектирование отсутствуют, в связи с чем границы среднечастотного участка могут быть выбраны до некоторой степени произвольно. Разумеется, этот участок должен иметь наклон -20дб/ден. Для получения приемлемого качества переходного процесса не следует ширину среднечастотного участка выбирать менее 0,3¸0,4 (в логарифмическом масштабе) причем частота среза должна располагаться приблизительно в середине этого участка.

Стыковка низкочастотного и среднечастотного участка, а также выбор формы высокочастотного участка ЖЛЧХ целиком находится в компетенции исполнителя. Выполнение следующих двух рекомендаций позволит избежать излишней сложности при реализации алгоритма управления:

-следует избегать ‘резких’ изломов асимптотической ЖЛЧХ,