Проектирование алгоритма управления электрогидравлическим приводом», страница 5

Результатом операции будет матрица значений корней(3.3) с числом строк равным числу элементов вектораК.

В (3.3) можно использовать как передаточную функцию W_u(z), так и передаточную функцию W_u(w). Понятно, что полиномы в RLOCUS должны соответствовать выбранной передаточной функции. При использовании W_u(z) условием устойчивости является нахождение корней (3.3) внутри единичной окружности с центром в начале координат, а при использовании W_u(w) для устойчивости системы все корни (3.3) должны находиться в левой полуплоскости. Первый вариант менее трудоемкий, т.к. нет необходимости в применении функции W2Z, но трактовка результатов более затруднительна, поскольку "на глаз" бывает довольно сложно определить, находится ли комплексный корень внутри единичной окружности. в любом случае значение К_р должно быть выбрано так, чтобы корни находились на некотором расстоянии от границы устойчивости.

После выбора значения K_р (аналитического или подбором) необходимо проверить качество переходных процессов в замкнутой системе с пропорциональным регулятором  и ее точность.

Качество переходного процесса оценивается по реакциям системы на ступенчатое изменение задающего воздействия. Передаточная функция замкнутой системы к задающему воздействию, приложенному на входе регулятора, имеет вид

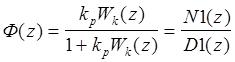    (3.4)

Полиномы N1 и D1 связаны с полиномами N и D передаточной функции W_k(z) очевидными соотношениями

N1=k_pN, D1=D+ k_pN,    которые непосредственно получаются из (3.4)

Реакция на ступенчатое воздействие вычисляется с помощью функции DSTEP :

Y=DSTEP(N1, D1, L)  L - число точек (периодов квантования)

По полученной переходной характеристике проверяется колебательность системы и время переходного процесса t_p , определяемое по вхождению в 3-5% окрестность установившегося значения. Если переходной процесс чрезмерно колебательный или излишне затянутый необходимо скорректировать значение к_р , добиваясь чтобы перерегулирование не превышало 30-40 % , а длительность переходного процесса была минимальной. График переходной характеристики должен быть приведен в пояснительной записке.

Точность следящей системы оценивается по величине амплитуды установившейся ошибки при отработке синусоидального задающего воздействия. Параметры задающего воздействия (частота и амплитуда) определены в задании. Передаточная функция следящей системы Ф_q , связывающая ошибку с задающим воздействием, находится по формуле

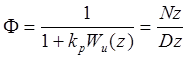      Nz=D,  Dz=D+K_pN

Для определения реакции системы нужно предварительно сформировать входное воздействие длительностью L периодов квантования, которое на (0,5 1,5) периодов синусоиды должно превышать определенное выше время переходного процесса. В среде MATLAB синусоидальный входной сигнал формируется следующим образом

I=0:1:L

UV=a*sin(w*TÆ*I)

График ошибки находится с помощью функции DLSIM:

TET=DLSIM(Nz, Dz, UV)

В некоторых исключительных случаях окажется, что полученные на этом этапе результаты удовлетворяют требованиям задания на проектирование. Вообще говоря, алгоритмическая часть проектирования на этом должна была бы закончится. Но, поскольку работа является учебной, в этом случае следует обратится к преподавателю за корректировкой задания.

 4. Синтез цифрового механизма

Алгоритм управления, реализуемый в цифровом регуляторе, должен быть выбран таким образом, чтобы система удовлетворяла требованиям задания на проектирование. Расчет алгоритма управления (иначе- алгоритм коррекции или закона управления) выполняется методом логарифмических частотных характеристик. Расчетная схема системы имеет вид  рис

Wu(z)

Wk(z)

                                 U                                            y_u