Язык начального обучения математике

8.  Козлов А.  С. Развивающее воспитание творчеством. - Новоси­
бирск: Рассвет, 1994. - Ч. 1. - 158 с.

9.  Нестеренко А. А. Страна загадок. - Ростов-на-Дону.: Изд-во Рос­
товского ун-та, 1993. - 32 с.

10 Никашин А. И., Страунинг А. М. Системный подход в ознакомле­нии с окружающим миром и развитии фантазии. - Ростов-на-Дону: Ас-

пект-ТРИЗ, 1993. -• 32 с.

11.  Сборник творческих задач по биологии экологии и ТРИЗ: Учеб­
ное пособие / Авт.-сост. В. И. Тимонов. - Санкт-Петербург: Изд-во ТОО
"ТРИЗ-ШАНС", 1996. - 105 с.

12.  Учебные задачи по ТРИЗ: Методические рекомендации к курсу
"Теория и практика научно-техническбго творчества" / Сост. Ладош-
кин В. С. - Новосибирск: "АЛГО", 1989. - 89 с.

13.  Царева С. Е. Обучение решению текстовых задач, ориентирован­
ное на формирование учебной деятельности младших школьников. -
Новосибирск: Изд-во НГПУ, 1998. - 136 с.

14.  Царева С. Е. Гуманитаризация содержания образования: сущ­
ность, пути и средства реализации // Вопросы совершенствования про­
фессиональной   подготовки  учителя  на  современном   этапе  развития
высшей школы: Сборник научных трудов. - Новосибирск: Изд-во НГПУ,

1997.-289 с.

15.  Шустерман 3. Г. Новые приключения Колобка, или наука ду­
мать для больших и маленьких. - М.: Педагогика-Пресс, 1993. - 256 с.

УДК

Е. А. Рудакова

Новосибирский государственный педагогический университет

ЯЗЫК НАЧАЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ

В статье рассматривается математический язык как совокупность знаков вербального и невербального характера. Приводится классифи­кация символов и знаков математического языка.

В обучении любому предмету используются естественный, разговорный^ язык и язык соответствующей предмету науки. В обучении математике наряду с естественным языком необходимо использование специального языка математики - математическо­го языка. При этом следует различать собственно математический язык (язык науки математики) и язык преподавания (изложения) математики. О различии этих языков говорили В. В. Мадер [5] и Г. В. Дорофеев [1].

Для построения каждой научной теории нужен свой язык, спе­цифический. Этот язык служит для описания предметной области данной теории. В. В. Мадер называет такой язык "предметным" [5]. Например, язык арифметики натуральных чисел описывает пред­метную область, состоящую из множества натуральных чисел. В этот язык входят символы операций сложения и умножения, "1^_-единицы натурального ряда, "<" - отношения_порядка и_ др. Такой предметный язык соответствует, согласно теории В. В. Мадера, первому уровню познания. На втором уровне создается так называ­емая метатеория, которая исследует ранее созданную предметную теорию. Для ее описания используется специальный "метаязык". "Он имеет предметную область, состоящую из символов исходного языка и объектов, необходимых для описания того или иного язы­кового аспекта" [5]. И предметный, и метаязык используются для описания готовой теории. "Иначе обстоит дело, если мы выражаем наше отношение к теории -размышляем, ставим вопросы, думаем, удивляемся, сомневаемся, уточняем смысл, то мы имеем делос не­формальным языком математики. Это уже не собственно математи­ческий язык, а язык изложения математики, язык исследователя, язык учителя" [5]. А. А. Столяр отмечает, что "в школьном обуче­нии мы применяем, как правило, словесно - символический язык, включающий элементы и символического языка математики, и ес­тественного словесного языка" [7, с. 38]. Этот язык, кроме собствен­но математического содержания, способен выразить и некоторые аспекты психологического характера, а также деятельностные ас-пекты изучения математики. В этом языке имеют место такие тер­мины, как "упростить выражение", "найти значение выражения", "решить уравнение" и др., не являющиеся терминами математичес-

кого языка. "В собственно математический язык они не входят, - счита­ет Г. В. Дорофеев, - по крайней мере, по двум причинам - логической и лингвистической: для математики они недостаточно корректны, и, кро­ме того, в математическом языке нет целевых указаний или повелитель­ного наклонения, возникающего при переформулировке этих требований в виде "упростите", "докажите" и т. д." [1, с. 39]. Однако такие предло­жения - требования, сформулированные на естественном языке, явля­ются достаточно ясными и доступными для понимания. Кроме того, в преподавании математики невозможно обойтись без такого рода фор­мулировок.

Из вышеизложенного следует, что обучение математике, в том числе и обучение начальному курсу математики в младших классах школы, предполагает использование некоторого комби­нированного языка. Заметим, что в методической литературе для его обозначения вводятся разные термины: "язык изложения математики" (В. В. Мадер [5]), "язык преподавания математики" (Г. В. Дорофеев [1, с. 38]), "язык математических описаний школь­ного курса математики" (Л. С. Оксман [6, с. 5]), "язык обучения математике" (Дж. Икрамов [3]). В связи с тем, что обучение мате­матике, на наш взгляд, не исчерпывается только изложением, пре­подаванием или описанием, в данной статье мы будем использо­вать термин Дж. Икрамова, расширенный применительно к на­чальной школе - "язык начального обучения математике".

Под языком начального обучения математике будем понимать совокупность некоторой области естественного языка, средств ма­тематического языка и дидактического языка, с помощью которых осуществляется обучение математике в начальных классах (рис. 1).

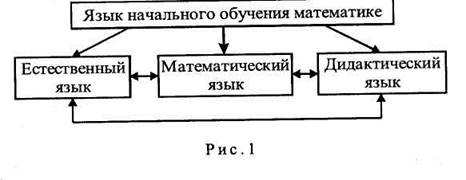
Рассмотрим более подробно составляющие компоненты языка на­чального   обучения   математике.

Под естественным языком понимают обычный разговорный язык какого-либо народа (русский, немецкий, японский и др.). Та­кой язык предназначен, прежде всего, для повседневного общения людей. Начальное обучение математике строится на базе естествен­ного языка. Причем, он является преобладающим по сравнению с математическим языком. Именно с помощью естественного языка возможно описание математических понятий, их свойств. Знаком­ство с математическими объектами должно быть каким-то образом отражено в речи детей. При этом первоначально учащиеся описы­вают математические понятия на естественном языке, постепенно переходя к использованию для этих целей математического языка. Основным "подъязыком" [1, с. 39] языка начального обучения математике является математический язык. В методической лите­ратуре существуют различные определения математического язы­ка. Так, Дж. Икрамов термин "математический язык" употребляет для обозначения "совокупности всех языковых средств, с помощью которых выражается математическая мысль" [2, с. 5]. При этом Ик­рамов рассматривает математический язык в качестве сложной сис­темы, включающей в себя много "подъязыков": язык математичес­ких символов, геометрических фигур, графиков, диаграмм, а также Элементов естественного языка [2, с. 6]. Н. Н. Левшин под матема­тическим языком понимает "систему, включающую средства род­ного языка, математическую терминологию, символику, схемы, графики" [4]. При этом, исходя из концепции знакового характера языка, он выделяет в качестве компонентов математического язы­ка семантику и синтаксис. В определении математического языка Л. С. Оксман эти компоненты также нашли отражение: "Матема­тический язык представляет собой совокупность всех терминов, слов, символов, из которых состоят математические предложения, и правил их употребления, определяемых смыслом элементов язы­ка и законами математики" [6, с. 4]. Л. М. Фридман определяет ма­тематический язык как "систему математических знаков и симво­лов, операции с которыми совершаются по особым правилам, уста­навливаемым в математике" [9, с. 112].