Язык начального обучения математике, страница 2

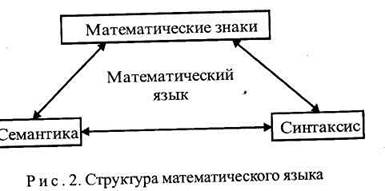
Суммируя вышеизложенные определения и также учитывая знако­вый характер языка, в данной статье под математическим языком будем понимать совокупность знаков вербального и невербального характера, с помощью которых выражается математическое содержание, и организованную в соответствии с определенными правилами семантики и синтаксиса (рис. 2).

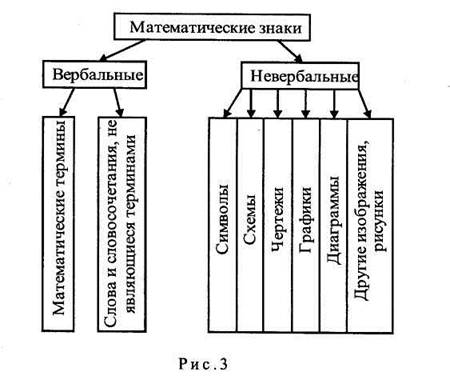
К вербальным знаковым единицам математического языка отно­сятся ма^гтатиде^кие_тер_минь1 и другие слова и словосочетания ес-тественного языка, необходимые для номинации математических объектов и математических описаний. Основные вербальные матема-тические знаки - это термины. В "Лингвистическом энциклопедичес­ком словаре" дано следующее определение термина: "Термин (от лат.   i terminus - предел, граница) - слово или словосочетание, обозначаю­щее понятие специальной области знания или деятельности" [8, с. 508]. В совокупности термины какой-либо научной области образуют ее терминологию - словарный запас, используемый в той или иной облас- ; ти науки для обозначения специфических объектов. Термин непосред- jj ственно связан с понятием, представляя собой его языковую оболочку.' Среди математических терминов можно выделить термины математи­ческих объектов ("трапеция", "треугольник", "уравнение", "неравен­ство", "функция", "цифра", "число" и др.), операций (сложение, диффе­ренцирование, умножение, логарифмирование и др.) и отношений (больше, меньше, параллельность, следование, делимость и др.).

Невербальные знаки математического языка объединяют в себе математические символы, схемы, чертежи, графики, диаграммы,

248                                                                                                                                   *

изображения геометрических фигур и т. п. Наличие математических символов является характерной чертой математического языка. Бо­лее того, именно математические символы, правила построения из них математических предложений, их преобразования, правила определе­ния их значений составляют главную часть математического языка. Для ученых-математиков элементы естественного языка, сопровож­дающие символьный язык, являются несущественными, служебными, и потому не включаются в математический язык. В обучении же есте­ственный язык является необходимой частью математического язы­ка, он оттеняет, дополняет язык символов.

Язык математики не исчерпывается лишь математической симво­ликой, его знаковый набор значительно многограннее (рис. 3).

И все же именно использование специальной символики сделало математический язык таким продуктивным и эффективным аппаратом как для самой математики, так и для других наук, каковым он явл­яется    в    настоящее    время.    Значение    символов    трудно    пе-

249

реоценить. Их использование позволяет значительно сократить за­пись, сделать ее более доступной для понимания и усвоения, помо­гает четко и лаконично отразить результаты исследований и т. п. Кроме того, "некоторые разделы математики вообще невозможны без начертания символов, которые позволяют записывать в ком­пактной и легкообозримой форме предложения, выражение кото­рых на обычном языке было бы крайне громоздким" [6, с. 8].

Под математическими символами будем понимать знаки, ус­ловно обозначающие в письменной математической речи матема­тические объекты, понятия, отношения и т. п. Первыми математи­ческими символами были знаки для записи чисел - цифры. Зачат­ки буквенного обозначения величин появились в III веке, когда Диофант ввел обозначения для неизвестной величины. Широкое применение прописных букв латинского алфавита в алгебре нача­лось с Виета (XVI в.), строчные буквы этого алфавита в математи­ку ввел Р. Декарт (XVII в.), символы для обозначения функций были введены Эйлером и т. д. Современная символика математи­ки создавалась веками, получая на протяжении столетий свое раз­витие при участии многих великих ученых.

Все математические символы можно разделить на следующие

группы:

-  символы объектов (5, X, 0, π, ∞ и т. п.);

-  символы операций (+, √ , ∩, V и т. п.);

-  символы отношений (=>, =,>,<,┴ и т. п.);

-  вспомогательные символы, устанавливающие порядок соче­
тания основных символов (скобки, запятая для записи десятичных

дробей и т. п.).

Совокупность всех математических символов образует алфа­вит формального математического языка. Так как математичес­кий язык включает в себя множество "подъязыков", то в его алфа­вите можно выделить несколько составляющих его алфавитов: арифметики, алгебры, логики высказываний, теории множеств, дифференциального и интегрального исчислений, аналитической

геометрии и др.

Отличные от математических символов невербальные знаки математического языка (схемы, графики, чертежи, диаграммы и

250

др.) являются графическими средствами выражения математичес­кого содержания и служат, в большей степени, для наглядного представления математических объектов и зависимостей.

Таким образом, знаковые единицы математического языка можно объединить в три группы: алфавит (символика), словарь (терминология) и графические невербальные средства, отличные от символов.