Язык начального обучения математике, страница 3

Все знаки математического языка определенным образом организованы. Отношения между ними устанавливаются в соот­ветствии с синтаксическими правилами. Под синтаксисом пони­мают тот аспект языка, который заключается в связи языковых знаков в высказывании и предложении. Если синтаксис словар­ного запаса математического языка практически совпадает с синтаксисом естественного языка,-Yo с невербальными знаками дело обстоит несколько иначе, хотя и существует определенная аналогия. Слово в формальной математике понимается так же, как и в естественном языке, то есть как последовательность букв (символов) алфавита, имеющая смысл. Например, записи (7,8 + 4)х5; 35; За + 4; a _L b являются словами математического языка, а записи 18 _1_ А; 8 + х9а; 56² : % 65 не имеют смысла, а значит, не являются словами. Из слов так же, как и в естествен­ном языке, составляются предложения. Ими в математическом языке служат равенства, неравенства, формулы и т. п. Например, следующие записи являются предложениями математического языка: 38а + 4 > 50; х = 5; (a _L с л а X Ь) => с || Ъ. Связь слов мате­матического языка в предложения осуществляется посредством символов операций и отношений, а также вспомогательных сим­волов порядка выполнения операций.

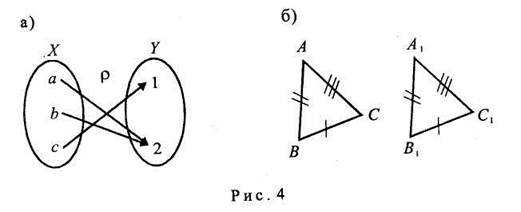
Для невербальных математических знаков, отличных от сим­волов, также устанавливаются определенные синтаксические правила. Так, например, соответствующие элементы пар ото­бражения на графе принято изображать стрелками, направлен­ными от первой компоненты ко второй (рис. 4а) соответствен­ные стороны равных фигур отмечаются одинаковыми значка­ми (рис. 46) и т. п.

251

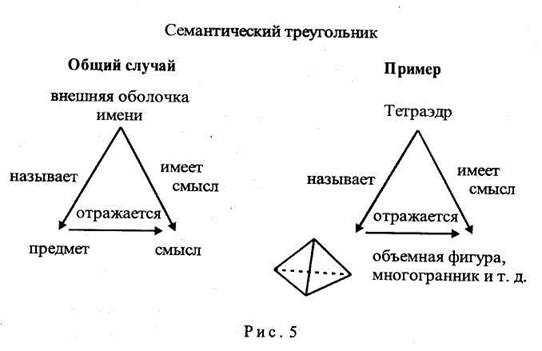
Семантический аспект математического языка проявляется в установлении значений и смыслов языковых единиц. Всякий предмет в математике имеет в математическом языке "имя" (термин В. В. Мадера [5]). При этом под предметом будем по­нимать не только отдельные объекты (треугольник, число во­семь, шар и т. п.), но и процессы - операции (интегрирование, дифференцирование и т. п.), а также и мыслимые предметы (бесконечность). Имя предмета имеет свою внешнюю оболоч­ку. Оно может быть выражено фонетическим словом - терми­ном, быть записано на естественном языке, выражено символи­ческим или другим графическим знаком. Кроме того, каждое имя в математическом языке имеет свой смысл. Таким образом, слово или имя в математическом языке есть комплекс, состоя­щий из предмета, внешней оболочки и смысла. Все три элемен­та этого комплекса связаны между собой: имя называет или обозначает предмет, имя имеет смысл, смысл отражает свой­ства предмета в сознании человека. Комплексное содержание имени может быть представлено схемой, называемой семанти­ческим треугольником (рис. 5).

Таким образом, семантика математического языка раскрыва­ет комплексное содержание каждого математического имени.

Исходя из вышеизложенного, можно заключить, что матема­
тический язык имеет свою четко организованную структуру: ал­
фавит, словарь, синтаксис и семантику. Заметим, что представ­
ленный анализ данной структуры не претендует на семиотичес­
кую точность и полноту.                                                                    I

252                                                                     ,          >                        1

В обучении математике математический язык играет двоя­кую роль. Математический язык является неотъемлемой частью науки математики. Поэтому в обучении математике использо­вание ее языка является необходимым условием. Без примене­ния средств математического языка описание математических объектов, раскрытие содержания математических понятий мак­симально затруднено. Кроме того, часто в математических зна­ках (терминах, символах и т. п.) отражен смысл математических понятий, что значительно облегчает процесс усвоения и поня­тий, и их обозначений. Математический язык в этой связи явля­ется одним из основных средств обучения математике. И полу­чение, и усвоение математических знаний во многом определяет­ся умением правильно составлять цепочки рассуждений в соот­ветствии с законами математического языка. Математический язык является также и средством развития мышления младшего школьника.

Роль математического языка как средства развития мышления школьников и формирования математических понятий, как опера­тивного аппарата изучения математики признана многими специа­листами в области методики преподавания математики: Б. М. Гне-

253

денко, В. А. Далингером, Дж. Икрамовым, А. Н. Колмогоровым,    |
С. Крыговской, Н. Н. Левшиным, А. И. Маркушевичем и др.       ]

Для того, чтобы эффективно использовать математический   ']
язык в качестве средства изучения математики, необходимо им    _;
владеть. Следовательно, математический язык должен быть и це­
лью обучения математике.|

Математический язык в начальном обучении математике мо­жет быть представлен по-разному. Причем различия могут быть  з не только в наборе изучаемых математических знаков, но и в под- 5 ходах к их изучению и использованию. Выбор того или иного i фрагмента математического языка для использования в началь- '■' ном обучении математике определяется и довольно ограничен­ным промежутком времени обучения, и возможностями усвоения компонентов математического языка младшими школьниками, и содержанием программы, по которой осуществляется обучение.