Контрольная работа № 2. Отчет по задачам: «Построение уравнения множественной регрессии» и «Многокритериальная оптимизация», страница 8

2.МНОГОКРИТЕРАЛЬНАЯ ОПТИМИЗАЦИЯ

2.1.Задание

Оценить альтернативы, характеристики которых по четырем критериям даны в таблице 5. «Веса» критериев по вариантам приведены в таблице 6. В таблице 6 также указано, что желательно сделать с данным критерием (символ - желательно уменьшить критерий, -увеличить).

Таблица 5

Альтернативы	Значения критериев по альтернативам
1	4	6	6	3
2	3	2	5	5
3	7	5	8	7
4	4	4	7	6
5	5	3	4	4
6	8	7	6	5
7	7	6	7	5
8	6	5	3	3
9	3	4	8	2
10	8	3	5	5

Таблица 6

Требуется:

1.  Построить множество решений оптимальных для Парето.

2.  Найти оптимальные альтернативы с помощью аддитивной функции ценности. Их целесообразно искать только среди решений оптимальных для Парето.

3.  Найти оптимальные альтернативы с помощью метода главного критерия. В таблице 6 символом * отмечен главный критерий.

4.  Решить задачу, используя метод идеальной точки. Использовать метрики (S=1), (S=2), (S=∞).

5.  Сделать окончательный вывод об оптимальной альтернативе.

2.2.Решение

2.2.1.Множество решений, оптимальных по Парето

В области компромиссных решений нельзя достигнуть одновременного улучшения решения по всем критериям. Область компромиссов является областью оптимальных решений по Парето.

Введем вектор показателей  составленный из значений критериев, при этом каждому допустимому варианту решения (альтернативе) соответствует свой вектор.

Вектор значений показателей  из области допустимых значений называют эффективным или оптимальным по Парето, если не существует другой такой точки в области допустимых значений, которая по всем параметрам была бы не хуже  и превосходила его хотя бы по одному.

В нашем случае сопоставляются 10 вариантов решений (альтернатив) по четырем критериям, из них  и  надо минимизировать, а  и - максимизировать. На рис. 14 и рис.15 представлена геометрическая интерпретация альтернатив.

Как видно из рис. 14 оптимальными по Парето являются альтернативы 2,5,8, но они не являются оптимальными исходя из графика, размещенного на рис. 15. Также из рис. 15 можно сказать, что альтернативы 3,4,6 оптимальны по Парето, но не оптимальны исходя из графика на рис. 14. 

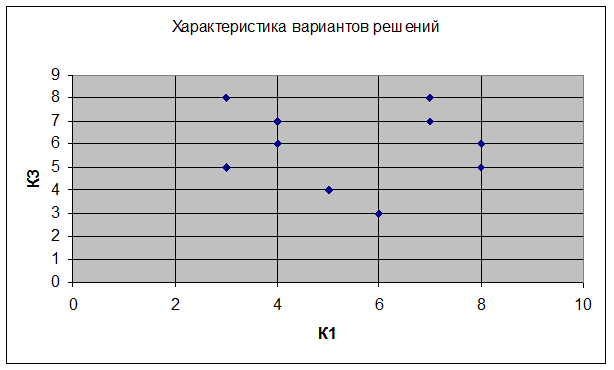
Рис. 14. Геометрическая интерпретация критериев, которые необходимо минимизировать

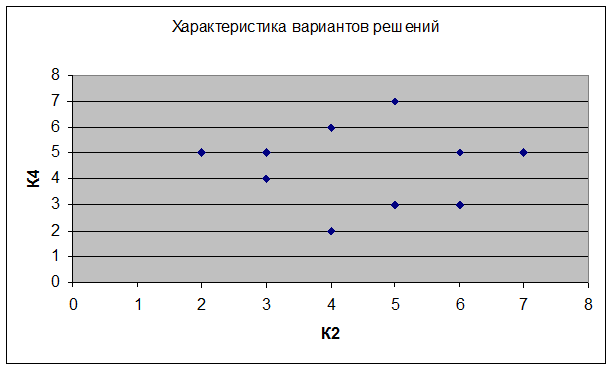
Рис. 15. Геометрическая интерпретация критериев, которые необходимо максимизировать

Рассмотрим 10 альтернатив аналитически, сравнивая варианты решений  друг с другом,

Чтобы удостовериться, что оптимальными по Парето являются все 10 альтернатив.

1. Сравниваем 1-ую альтернативу:

- с 2-ой, обнаруживаем, что 2 альтернатива лучше по ,,;

- с 3-ей, обнаруживаем, что 3 альтернатива лучше по ;

- с 4-ой, обнаруживаем, что 4 альтернатива лучше по ,;

- с 5-ой, обнаруживаем, что 5 альтернатива лучше по ,;

- с 6-ой, обнаруживаем, что 6 альтернатива лучше по ,;

- с 7-ой, обнаруживаем, что 7 альтернатива лучше по;