Контрольная работа № 2. Отчет по задачам: «Построение уравнения множественной регрессии» и «Многокритериальная оптимизация», страница 4

Рис. 4.

Полученные числа имеют следующий смысл, представленный в таблице 3:

Таблица 3

S_e – стандартная ошибка для коэффициента m;

S_eb – стандартная ошибка для свободного члена b;

R² – коэффициент детерминированности, который показывает как близко уравнение описывает исходные данные. Чем ближе он к 1, тем больше сходится теоретическая зависимость и экспериментальные данные.

S_ey – стандартная ошибка для y;

F – критерий Фишера определяет случайная или нет взаимосвязь между зависимой и независимой переменнымы;

Df – степень свободы системы;

Ssreg – регрессионная сумма квадратов;

Ssresid – остаточная сумма квадратов.

Таким образом, в классе однофакторных регрессионных моделей наиболее информативным предиктором (предсказателем) является  (табличная функция ЛИНЕЙН показала, что R²=0,8716)- общая площадь квартиры. Включим эту переменную в выстраиваемую методом включения модель.

Вычислим скорректированный коэффициент детерминации при k=1:

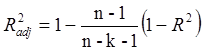                                                                (2)

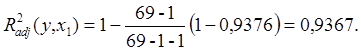
2-й шаг (k=2). Среди всевозможных пар , выбираем наиболее информативную (в смысле  или, что то же самое, в смысле ) пара.

Последовательно применяем табличную функцию ЛИНЕЙН к различным парам:

Очевидно, что наиболее информативной парой является , которая дает

.

С включением параметра  коэффициент детерминации вырос, следовательно, это правильное решение. Линейное уравнение с учетом факторов  имеет вид:

.

Используя надстройку «Регрессия, проведем анализ значимости найденных коэффициентов

(рис.5).

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	0,597648128	0,85917455	0,695607346	0,489116913
х1	0,515346379	0,012197632	42,249707	1,65355E-49
х5	-0,330969116	0,046597167	-7,102773329	1,06313E-09

Рис.5. Фрагмент отчета регрессии по двум переменным

Столбец t-статистика содержит наблюдаемые значения t-критерия Стьюдента . Столбец «Р-значение» используется для проверки гипотезы :  (о незначимости i-го коэффициента регрессии) с помощью критерия Стьюдента. Столбец содержит вероятности того, что в силу случайных причин  принимает это или большее значение, хотя коэффициент регрессии . «Р-значение» сравнивается с выбранным уровнем значимости а, если «Р-значение» больше или равно а, то гипотеза подтверждается и коэффициент незначим. В противном случае коэффициент существенно отличен о  0, т.е. значим.  Рассмотрев столбец «Р-значение» (рис.4), приходим к выводу: два коэффициента при независимых переменных  статистически значимо отличаются от нуля при уровне значимости а=0,05. Коэффициент 0,5976 («Y-пересечение») не значим, и его следует исключить из уравнения.

Таким образом, уравнение имеет вид:

.

3-шаг (k=3). Попытаемся добавить третью переменную в наше уравнение регрессии. Среди всевозможных троек , выбираем аналогично 1 и 2 шагу наиболее информативную.

Наиболее информативной является , которая дает (3)=0,9650.

Вычислим частный критерий Фишера для оценки прироста факторной дисперсии, обусловленного включением в модель фактора :

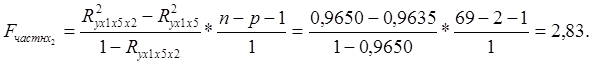                           (3)

 = вычислим с помощью табличной функции FРАСПОБР(0,05;1;69).

<=3,97.

Следовательно, третью переменную в модель включать нецелесообразно, т.к. она существенно не повышает значение .

Этот же результат получим, применив надстройку «Регрессия» (рис. 6).Отметим, что коэффициент  не значим.

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	0,337074321	0,852944835	0,395188888	0,693997444
х1	0,589092639	0,040157912	14,66940406	2,6705E-22
х5	-0,334189998	0,045702885	-7,312229756	4,85926E-10
х2	-0,127120945	0,066083794	-1,923632659	0,058782024