Контрольная работа № 2. Отчет по задачам: «Построение уравнения множественной регрессии» и «Многокритериальная оптимизация», страница 5

Рис. 6. Фрагмент отчета регрессии по трем переменным

Уравнение

адекватно описывает зависимость стоимости квартиры от влияющих на нее фактров, и может быть использовано для анализа и прогноза. Все коэффициенты при неизвестных в нем значимы.

1.2.4.Пункт 4.

Для  применения метода наименьших квадратов требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора  остатки  имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.

Рассмотрим графики остатков для переменных , полученных при построении уравнения регрессии с помощью надстройки «Анализ данных - Регрессия» (рис. 7).

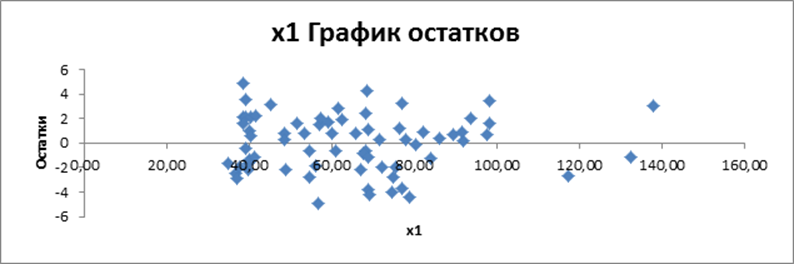
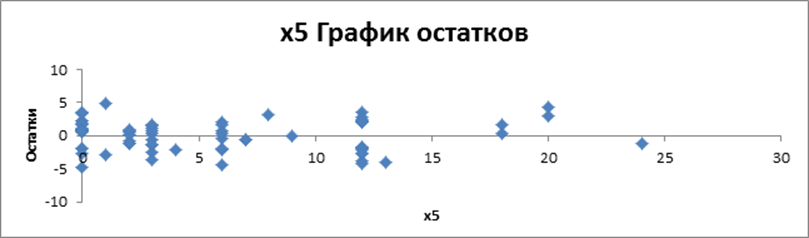
Рис. 7. Графики остатков

Нарушение гомоскедастичности может быть выявлено с помощью метода (теста) Гольфельда-Квандта. Предварительно все наблюдения упорядочим по одному из факторов, например, по .

Для применения теста Гольфельда-Квандта необходимо определить число исключаемых центральных наблюдений С. В рассматриваемом примере при n=69 было исключено 17 наблюдений (С=17). Тогда в каждой группе будет по 26 наблюдений.

Для первой группы наблюдений строим уравнение линейной регрессии с помощью функции ЛИНЕЙН(C3:C26;A3:B26;1;1) , которое представлено на рис. 8.

	для первой группы
	-0,33452	0,501022	1,439071
	0,088866	0,077739	3,266626
	0,673026	2,240877	#Н/Д
	23,67096	23	#Н/Д
	237,7288	115,4951	#Н/Д

Рис.8. Результат работы функции ЛИНЕЙН для первой группы наблюдений

Определяем остаточную сумму квадратов () для первой группы:  =115,4951.

Для первой группы наблюдений строим уравнение линейной регрессии с помощью функции ЛИНЕЙН(C44:C71;A44:B71;1;1) , которое представлено на рис. 9.

	для второй группы
	-0,40153	0,564691	-3,79739
	0,073915	0,02502	2,291811
	0,959968	2,250893	#Н/Д
	275,7718	23	#Н/Д
	2794,406	116,5299	#Н/Д

Рис.9. Результат работы функции ЛИНЕЙН для второй группы наблюдений

Определяем остаточную сумму квадратов () для первой группы:  =116,5299.

                                                                         (4)

 =FРАСПОБР(0,05;23;23)=2,01. Следовательно, <, значит, гипотеза о гомоскедастичности остатков не подтверждается.

Так как ошибки аппроксимации гетероскедастичны, применение МНК по данному условию некорректно. В этом случае следует помнить:

·  Стандартные ошибки будут занижены, что может привести к ложному выводу о значимости коэффициентов;

·  Полученные оценки коэффициентов являются несмещенными оценками, поэтому их можно использовать в  уравнении;

·  На практике стандартные ошибки пересчитываются с помощью известных методов Уайт, Ньюи-Вест.

1.2.5.Пункт 5.

Также для применения МНК требуется, чтобы значения остатков были распределены независимо друг от друга. Если это не так, то говорят, что остатки автокоррелированы.

Тестом на простейшую автокорреляцию ошибок (первого порядка) является тест Дарбина-Уотсона. В таблице 4  и на рис. 10. представлена организация данных для вычисления статистики Дарбина-Уотсона.

Таблица 4