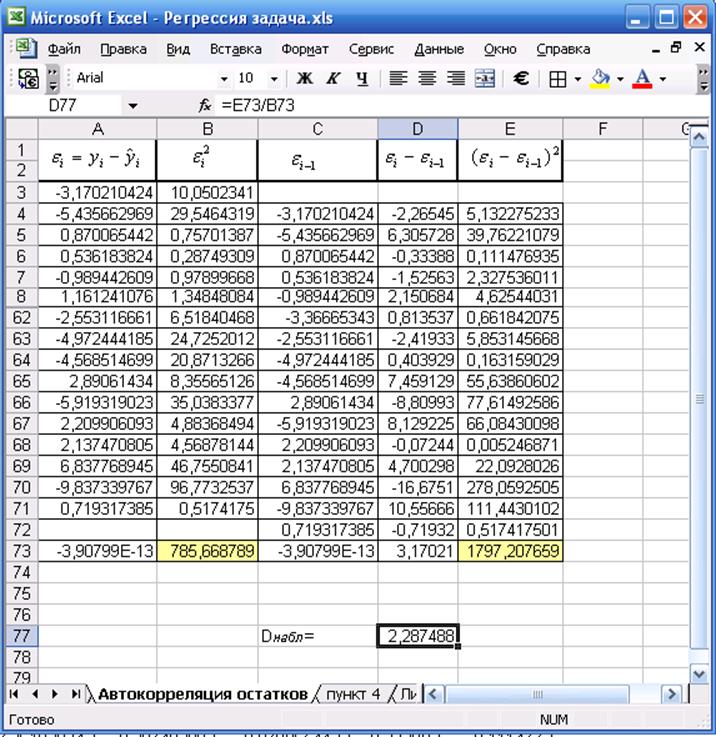
Рис.10. Организация данных для вычисления статистики Дарбина-Уотсона
По
таблице «Статистика Дарбина-Уотсона» для n=70
и k=2 находим критические значения ![]() и
и ![]() .
В нашем случае
.
В нашем случае ![]() , что превышает 2,
значит, это свидетельствует об отрицательной корреляции и перед сравнением эту
величину надо преобразовать:
, что превышает 2,
значит, это свидетельствует об отрицательной корреляции и перед сравнением эту
величину надо преобразовать:
![]() (5)
(5)
![]() .
.
Поскольку
![]() , т.е.
, т.е. ![]() ,
остатки некоррелированы, модель адекватна.
,
остатки некоррелированы, модель адекватна.
Так как значения остатков были распределены независимо друг от друга, применение МНК по данному условию корректно.
1.2.6.Пункт 6.
Выведем уравнение множественной регрессии в стандартизованном масштабе. Определим стандартизованные переменные:
 ;
(6)
;
(6)
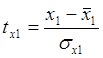 ;
(7)
;
(7)
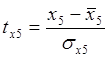 ;
(8)
;
(8)
где
![]() - среднее квадратическое отклонение,
- среднее квадратическое отклонение, ![]() ,(
,( ![]() -дисперсия);
-дисперсия);
![]() - условные средние данные.
- условные средние данные.
Воспользуемся табличными формулами ДИСП, КОРЕНЬ и СУММ, как показано на рис. 11.
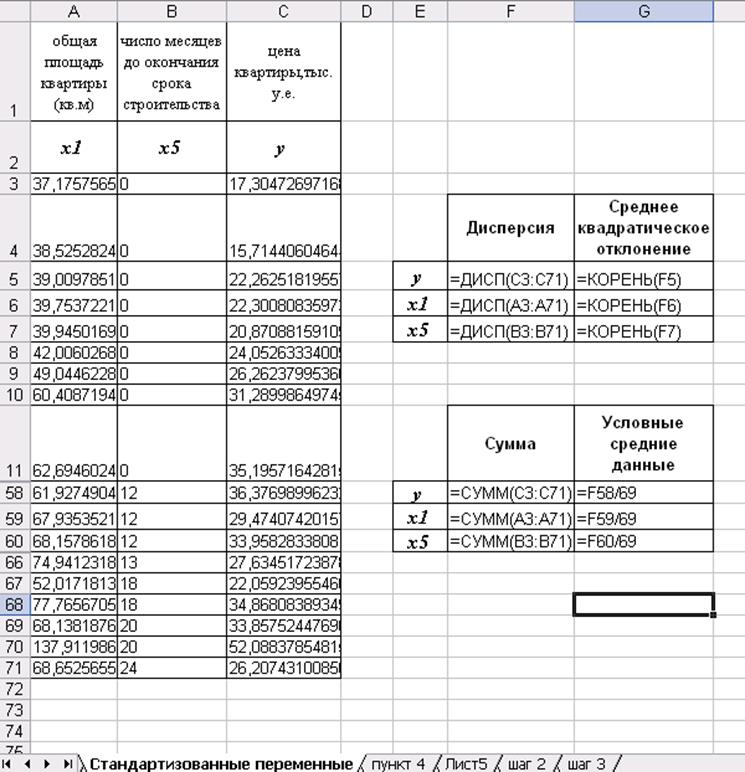
Рис. 11. Режим представления формул
На рис. 12 показаны числовые значения дисперсии, средних квадратических отклонений и условных средних данных.
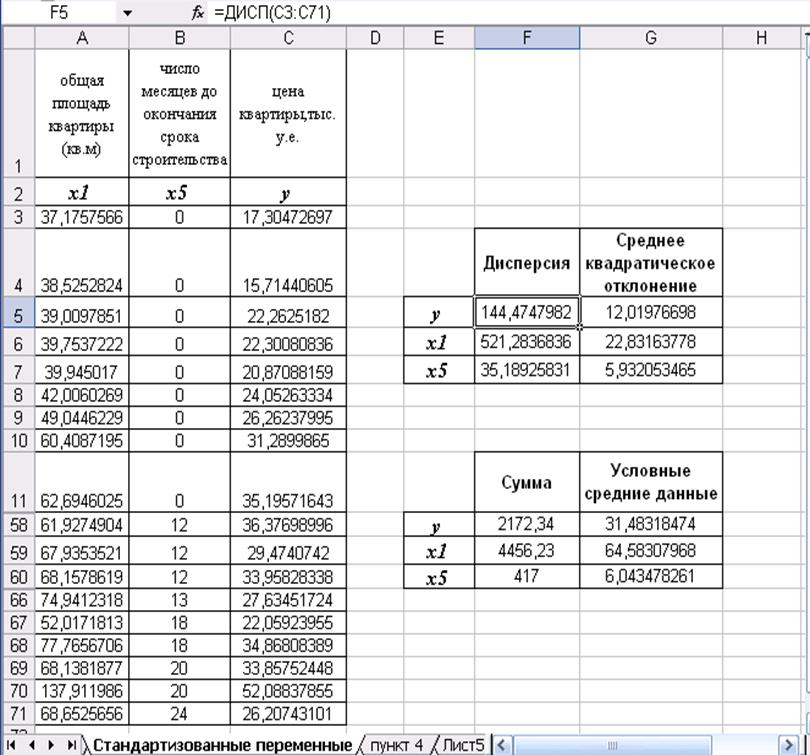
Рис. 12.
Также
можно воспользоваться надстройкой «Анализ данных – Описательная статистика»
рис.13.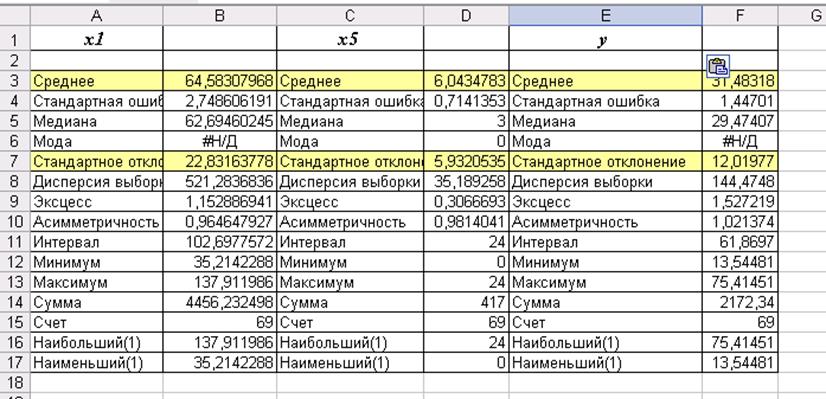
Рис. 13. Отчет «Описательная статистика»
Вычислим стандартизованные переменные:
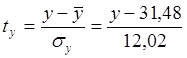 ;
; 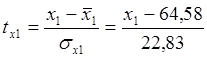 ;
;
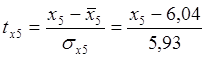 .
.
Для
определения коэффициентов стандартизованного уравнения множественной регрессии
![]() можно использовать МНК или воспользоваться
связью стандартизованных коэффициентов с полученными ранее коэффициентами
множественной регрессии.
можно использовать МНК или воспользоваться
связью стандартизованных коэффициентов с полученными ранее коэффициентами
множественной регрессии.
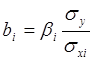 (9)
(9)
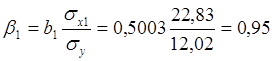 ;
; 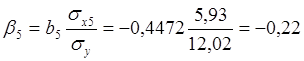 .
.
Таким образом, уравнение множественной регрессии в стандартизованном масштабе имеет вид:
![]() .
.
В силу того, что стандартизованные переменные центрированные и нормированы, стандартизованные коэффициенты можно сравнить между собой, т. е. сравнить факторы по силе воздействия. В нашем случае влияние первого фактора на результат более, чем в четыре раза (0,95/0,22>4) превышает влияние пятого фактора.
1.2.7.Пункт 7
Рассчитаем средние частные коэффициенты эластичности по формуле:
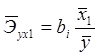 (10)
(10)
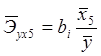 (11)
(11)
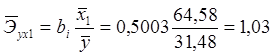 ;
; 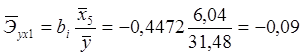 .
.
При
изменении фактора ![]() на один процент
результат возрастет на 1,03%, при неизменных прочих параметрах. Аналогично, при
изменении фактора
на один процент
результат возрастет на 1,03%, при неизменных прочих параметрах. Аналогично, при
изменении фактора ![]() на один процент
значение результатирующего фактора уменьшится на 0,09% при неизменных прочих
параметрах.
на один процент
значение результатирующего фактора уменьшится на 0,09% при неизменных прочих
параметрах.
Выводы:
·
Уравнение
![]() адекватно описывает зависимость стоимости
квартиры от влияющих на нее факторов и может быть использовано для анализа и
прогноза. Все коэффициенты в нем значимы.
адекватно описывает зависимость стоимости
квартиры от влияющих на нее факторов и может быть использовано для анализа и
прогноза. Все коэффициенты в нем значимы.
· Увеличение общей площади квартиры на 1 кв. м. приводит к увеличению стоимости квартиры на 500 у.е., увеличение (отдаление) срока сдачи на 1 месяц снижает стоимость квартиры на 447 у.е. Влияние прочих факторов несущественно.
· Влияние общей площади квартиры на ее стоимость более, чем в четыре раза превышает влияние срока сдачи объекта на стоимость.
· При изменении цены общей площади квартиры на один процент стоимость квартиры возрастет на 1,03%, при неизменных прочих параметрах. Аналогично, при изменении срока сдачи объекта на один процент стоимость квартиры уменьшится на 0,09%, при неизменных прочих параметрах.
· Проверка корректности применения МНК показала, что ошибки аппроксимации (значения остатков) гетероскедастичны, но распределены независимо друг от друга.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.