Другие предметы \ Экономико-математическое моделирование и оптимизация технологических процессов в шахтах

, страница 10

Следовательно, из 3-х других альтернатив не нашлось такого варианта решений, который был бы не хуже 7-ой альтернативы по всем критериям и превосходил бы хотя бы по одному. Значит, 7 вариант решений является оптимальным по Парето.

Сравниваем 8-ую альтернативу:

- с 9-ой, обнаруживаем, что 9 альтернатива лучше по ;

- с 10-ой, обнаруживаем, что 10 альтернатива лучше по ;

Следовательно, из 2-х других альтернатив не нашлось такого варианта решений, который был бы не хуже 8-ой альтернативы по всем критериям и превосходил бы хотя бы по одному. Значит, 8 вариант решений является оптимальным по Парето.

Сравниваем 9-ую альтернативу:

- с 10-ой, обнаруживаем, что 10 альтернатива лучше по ,;

Следовательно,9 и 10 альтернативы являются оптимальными по Парето.

Таким образом, приходим к выводу, что все 10 альтернатив являются оптимальными по Парето.

2.2.2.Аддитивная функция ценности

Основная идея количественных методов – введение единственного комплексного критерия оптимальности (функция ценности). Это позволяет свести проблему векторной оптимизации к одномерной (скалярной, одноцелевой) и, следовательно, однозначно оценить сравниваемые альтернативы.

Аддитивный метод в теории многокритериальной оптимизации принято называть свертыванием критериев.

Для соизмерения различных целей устанавливают относительные «веса» критериев, показывающие взаимоотношения между их шкалами, т. е. их важность. Чаще всего используется линейная функция ценности, которая вычисляется следующим образом:

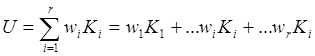, (12)

где i- индекс критерия оптимальности, i=1,2,…,r;

- вес (важность) i-критерия;

- значение i-критерия.

В нашем примере используются частные критерии. Поэтому целесообразно от значений частных перейти к нормированным значениям, которые мы вычислим по формуле:

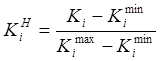, (13)

где - соответственно максимальное и минимальное значения i-критерия.

В таблице 7 приведены нормированные значения критериев.

Таблица 7

Альтернативы	Значения критериев по альтернативам

1	0,2	0,8	0,6	0,2
2	0	0	0,4	0,6
3	0,8	0,6	1	1
4	0,2	0,4	0,8	0,8
5	0,4	0,2	0,2	0,4
6	1	1	0,6	0,6
7	0,8	0,8	0,8	0,6
8	0,6	0,6	0	0,2
9	0	0,4	1	0
10	1	0,2	0,4	0,6

Размерности самих частных критериев и соответствующих нормирующих делителей одинаковы, поэтому в итоге обобщенный аддитивный критерий получается безразмерной величиной.

В аддитивной целевой функции ценности учитывается знак критерия. Если критерий учитывает отрицательные свойства, то он входит в функцию, ценности со знаком «минус». В нашем случае и будут со знаком «минус», т. к. значения этих критериев нужно минимизировать.

= -0,2*0,2+0,2*0,8-0,3*0,6+0,3*0,2=0;