Контрольная работа № 2. Отчет по задачам: «Построение уравнения множественной регрессии» и «Многокритериальная оптимизация», страница 3

1.2.2.Пункт 2.

Пользуясь надстройкой «Анализ данных - Регрессия» (рис. 1, 2) построим уравнение регрессии.

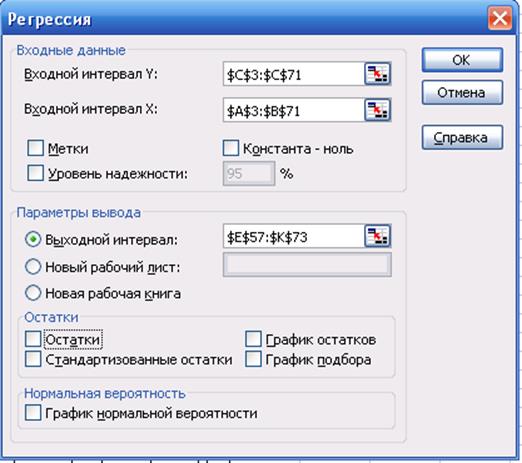
Рис. 1. Диалоговое окно надстройки  «Анализ данных - Регрессия»

Рис. 2. Фрагмент отчета регрессии по пяти факторам

Получили уравнение:

.

Очевидно, что полученное уравнение противоречит практике, коэффициент при  имеет знак «минус», то есть увеличение жилой площади уменьшает общую стоимость квартиры. Проанализируем межфакторную корреляцию. Для получения матрицы парных линейных коэффициентов корреляции воспользуемся надстройкой «Анализ данных – Корреляция» (рис. 3).

 Рис. 3. Корреляционная матрица

Значения коэффициентов линейной парной корреляции высоки , что говорит о взаимозависимости этих факторов, т. е. о мультиколлинеарности.

Полученное уравнение множественной регрессии, включающее весь имеющийся набор факторов, не адекватно. Возможная причина – мультиколлинеарность факторов, включенных в модель. Чтобы исключить взаимозависимые факторы, построим модель методом последовательного включения факторов.

1.2.3.Пункт 3.

Построение модели методом включения – это пошаговый отбор переменных.

На первом шаге (k=1) по наибольшему значению коэффициента корреляции с у найдем наиболее информативную переменную – это .

Так как при k=1 величина  совпадает с квадратом обычного (парного) коэффициента корреляции  из матрицы корреляций находим наибольший коэффициент детерминации для набора однофакторных регрессионных моделей:

Аналогичный результат можно получить последовательно строя уравнения регрессии для зависимостей  с помощью табличной функции ЛИНЕЙН (изв. зн. Y, изв. зн. X, константа, статистика) она возвращает массив значений описывающих кривую вида:

                                                (1)

Введем формулу в произвольный массив на листе MS Excel =ЛИНЕЙН(F3:F71;A3:A71;1;1). Поскольку функция возвращает массив, она должна задаваться в виде формулы массива при помощи комбинации клавиш <Ctrl> + <Shift> + <Enter>.

В результате получили полную статистическую информацию, применяя табличную функцию ЛИНЕЙН последовательно для каждого столбца (рис.4):