Контрольная работа № 2. Отчет по задачам: «Построение уравнения множественной регрессии» и «Многокритериальная оптимизация», страница 11

Как видно, наивысшую ценность имеют альтернативы 2 и 8. Отрицательные значения ценности не должны приниматься во внимание, ибо нас интересуют только сравнительная только сравнительная ценность альтернатив. Таковыми являются альтернативы 3,7, 9 и 10. Наличие отрицательных значений еще раз показывает условность функции ценности, отсутствие у нее в большинстве случаев реального экономического и технологического смысла.

2.2.3.Метод главного критерия

В методе главного критерия в качестве целевого функционала выбирается один из критериальных выходных параметров, наиболее полно с точки зрения исследователя отражающий цели оптимизаций. Остальные частные критерии оптимальности учитываются с помощью введения необходимых критериальных ограничений, определяющих совместно с прямыми и функциональными ограничениями допустимое множество. Основные трудности такого подхода связаны с проблемой назначения критериальных ограничений. Кроме того, в большом числе случаев всегда есть несколько главных критериев, находящихся в противоречии друг с другом.

Главным критерием является , а для 2-го, 3-го и 4-го критерия допустимыми уровнями будут 5, 5 и 4 соответственно.   и   нам следует уменьшить, а  и увеличить. В данном случае оптимальной альтернативой  3-му и 4-му критериям будет являться 2-я альтернатива. Также по главному критерию оптимальной альтернативой является 2-я. Но по главному критерию оптимальна и 9-ая альтернатива, но она не оптимальна по остальным критериям.  Следовательно, 2-я альтернатива являются оптимальной при заданных уровнях значимости и данном главном критерии.

2.2.4.Метод идеальной точки

Особую разновидность количественных методов решения многокритериальных задач представляют те, в которых ценность альтернатив определяется не на основе агрегирования оценок по отдельным критериям (построения функции ценности), а путем определения меры близости решения к некому идеальному (так называемой точке идеала, или идеальной точке). Т.е решение должно обеспечивать наибольшее приближение к множеству одновременно недостижимых целей.

Данный метод используется при различных метриках, функциях расстояния. В общем случае:

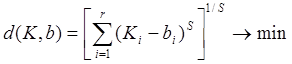                                    (14)

где - желательное значение i- того критерия;

S- характеристика метрики.

При S=2 вычисляется евклидово расстояние:

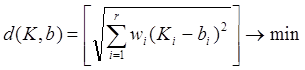                                     (15)

При S=1 задача сводится к минимизации суммы модулей относительных с учетом «веса» отклонений:

                                               (16)

При S=∞ имеем равномерную метрику, и задача целевого программирования сводится к минимизации максимального относительного отклонения, т.е.

                                                (17)

Таким образом, с помощью табличного процессора MS Excel введем следующие формулы в ячейку B20:

=КОРЕНЬ(($B8-$B$5)^2*$B$2+($C8-$C$5)^2*$C$2+($D8-$D$5)^2*$D$2+($E8-$E$5)^2*$E$2);

- в ячейку С20:

=ABS($B$5-$B8)*$B$2+ABS($C$5-$C8)*$C$2+ABS($D$5-$D8)*$D$2+ABS($E$5-$E8)*$E$2;

- в ячейку D20:

=МАКС(ABS($B8-$B$5)*$B$2;ABS($C8-$C$5)*$C$2;ABS($D8-$D$5)*$D$2;ABS($E8-$E$5)*$E$2).

Далее аналогично формулы вставляем по столбцам, и получим результат решения задачи методом идеальной точки (рис.16).

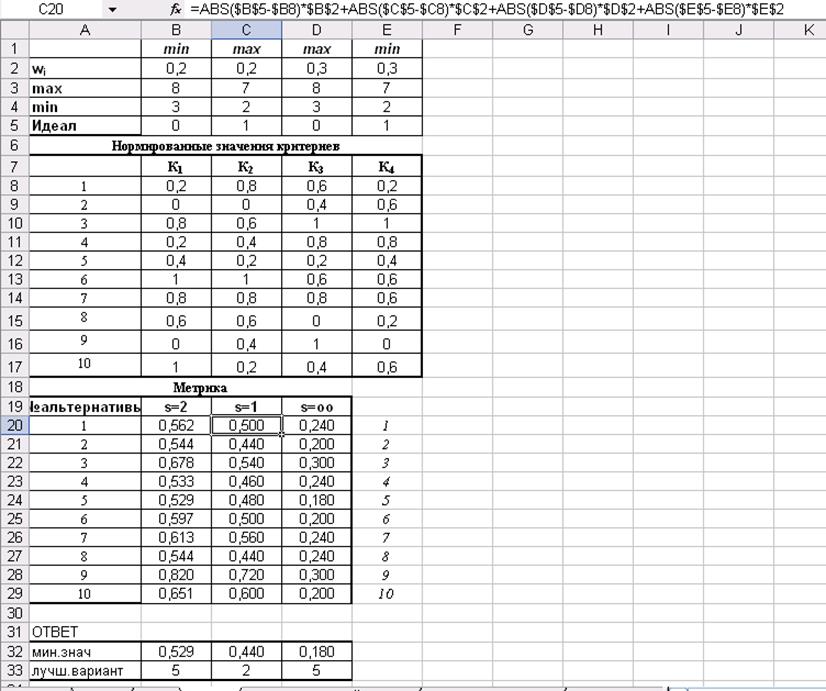
Рис.16

В данном примере лучшим вариантом по двум метрикам является альтернатива 5, по одной метрике альтернатива 2.

2.2.5.Вывод

В данном примере мы оценивали 10 альтернатив с 4-мя критериями, из них  и   нам следует уменьшить, а  и увеличить, по 4 методам:

·  По методу Парето все 10 альтернатив являются оптимальными.

·  По методу аддитивной функции ценности наивысшую ценность имеют альтернативы 2 и 8.

·  По методу главного критерия 2-я альтернатива являются оптимальной при заданных уровнях значимости и данном главном критерии.

·  По методу идеальной точки лучшим вариантом по двум метрикам является альтернатива 5, по одной метрике - альтернатива 2.