Конспект лекций по дисциплине "Прикладная фотограмметрия", страница 8

Ошибки определения элементов ориентирования исходной модели и систематические ошибки  соединения моделей (второе и третье слагаемое формул (9.15)) приводят к деформации маршрутной сети, которая с учетом переноса начала координат описывается алгебраическими полиномами вида

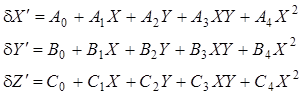                                                                     (9.16)

Если при выводе зависимостей (9.15) сохранить члены второго порядка малости ряда разложения тригонометрических функций, то деформация сети будет характеризоваться уравнениями вида:

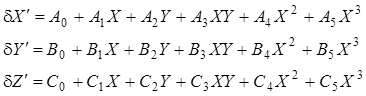                                                         (9.17)

Коэффициенты ,…., ,…., ,…. зависят от ошибок элементов ориентирования моделей маршрутной сети.

Для более полного учета влияния кривизны Земли в уравнения (9.16)и (9.17) можно ввести дополнительные слагаемые , , .

§79. Внешнее ориентирование и уравнивание маршрутной сети интерполяционным способом

Уравнения (9.16) и (9.17) описывают деформацию маршрутной сети, обусловленную систематическими погрешностями ее построения. Из выражения (9.15) видно, что деформация сети вызывается также и случайными погрешностями ее построения. Совместное действие этих погрешностей приводит к сложной деформации, уравнения которой могут быть установлены только при наличии достаточно большого числа равномерно расположенных опорных точек или при наличии истинных элементов внешнего ориентирования снимков.

На основании экспериментальных исследований и производственных работ установлено, что в сетях пространственной фототриангуляции случайные погрешности элементов ориентирования в результате их двойного суммирования (последнее слагаемое уравнений (9.15)) также приводят к относительно закономерной деформации. Так, при многократном построении сети по одним и тем же снимкам на одном и том же приборе и одним и тем же исполнителем величина ее прогиба меняется, но его изменение при переходе от модели к моделе по заданному направлению происходит по плавной кривой. Такой характер изменения деформации сети позволяет использовать для ее учета уравнения (9.16) и (9.17).

Схемы расположения опорных точек при уравнивании маршрутной сети по формулам (9.16) показаны на рис. 9.3., а по формулам (9.17) – на рис.9.4.

Уравнивание координат производится раздельно. Для уравнивания маршрутной сети сначала необходимо привести геодезическую систему координат в соответствие с фотограмметрической системой . Затем по формулам преобразования координат геодезические координаты  перевычисляются в фотограмметрическую систему координат. Масштаб преобразования и элементы ориентирования находятся по координатам минимум трех опорных точек, расположенных на исходной модели сети. Элементы ориентирования находятся аналитическим путем. Имея условные геодезические и фотограмметрические координаты опорных точек, находят невязки и составляют три системы уравнений поправок, например, вида:

,

,

.

Число уравнений, входящих в каждую систему, определяется числом используемых опорных точек.

Решая отдельно каждую систему уравнений поправок при условии , находят коэффициенты .

Уравненные координаты точек маршрутной сети вычисляются по формулам:

Полученные координаты точек фотограмметрического сгущения затем преобразуются в геодезические координаты. Для этого их приводят в соответствие с геодезической системой. Элементы внешнего ориентирования находят по координатам опорных точек.

Описанный способ уравнивания маршрутной фототриангуляции называется интерполяционным способом.

Если фотограмметрическая сеть имеет значительную длину, простираясь в нескольких зонах системы координат Гаусса, то для ее внешнего ориентирования и уравнивания используют координаты опорных точек в прямоугольной промежуточной системе координат  (§ 14 учебного пособия «Фотограмметрия», СПб 2006г.). Координаты точек в этой системе  получаются путем преобразования их координат в геоцентрической системе, которые в свою очередь находятся путём преобразования координат Гаусса по формулам, известным из курса высшей геодезии.

§80. точность пространственной фототриангуляции