Конспект лекций по дисциплине "Прикладная фотограмметрия", страница 7

§78. уравнения искажений координат точек свободной маршрутной сети пространственной фототриангуляции

Маршрутные сети пространственной фототриангуляции в процессе их построения деформируются. Деформация маршрутной сети вызывается ошибками снимка, прибора и наблюдателя.

В аналоговой, аналого-цифровой и в аналитической (способ моделей) элементарным звеном является одиночная модель. Совместное влияние различных источников ошибок приводит к искажению координат точек одиночных моделей и погрешностям определения относительных элементов внешнего ориентирования, посредством которых одиночные модели объединяются в модель маршрута.

Погрешности определяемых элементов ориентирования состоят из двух частей: систематической и случайной. К основным источникам погрешностей, вызывающих систематические искажения элементов ориентирования, относится дисторсия объектива АФА, невыравнивание пленки в плоскость в момент экспозиции, деформация пленки, рефракция, кривизна поверхности Земли, клинообразность светофильтра и т.д. Случайная часть искажений вызывается случайным отклонением пленки от плоскости в момент фотографирования, отклонением расположения точек ориентирования от стандартной схемы, ошибками опознавания точек ориентирования на смежных моделях и ошибками наблюдений.

Вывод уравнений искажений координат точек выполним для свободной сети пространственной фототриангуляции, построенной путем образования одиночных моделей и соединения их в модель маршрута.

Примем, что построение одиночных моделей и их соединение в маршрутную сеть выполнено безошибочно. Тогда условные геодезические координаты точки маршрутной сети вычисляются по формулам:

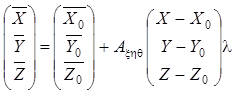                                                                                               (9.13)

где , ,  и  - условые геодезические и фотограмметрические координаты опорной точки исходной модели, принятой за начало координат; - фотограмметрические координаты точки сети; -условные элементы внешнего ориентирования (модели) сети; - матрица преобразования координат  в систему координат , , ;  - масштабный коэффициент (модели) сети.

Численные значения элементов матрицы  рассчитываются через углы .

Однако в действительности процесс создания моделей и присоединения каждой последующей модели к предыдущей сопровождается погрешностями, приводящими к постепенному изменению их элементов ориентирования.

Обозначим элементы ориентирования -ой модели  через а матрицу преобразования  через . Тогда пространственные координаты точки -ой модели маршрутной сети в системе координат исходной модели определяют по формулам:

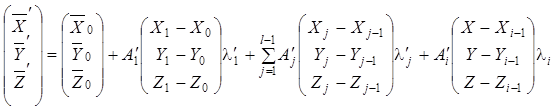,                  (9.14)

где   координаты го центра проекции ой модели маршрутной; X, Y, Z – координаты точки, расположенной в i-ой модели маршрутной сети.

Параметры начальной и -ой модели связаны с их истинными значениями  зависимостями:

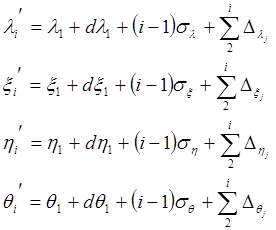  где ,  - соответственно систематическая и случайная составляющие погрешности одной передачи элемента ориентирования модели;

, , ,  - случайные погрешности определения параметров , ,  и  начальной модели.

Очевидно, что разности координат  - ,  - ,  -  точки маршрутной сети представляют собой истинные ошибки ее положения в плане и по высоте. Обозначив эти ошибки соответственно через , ,  и учтя выражения (9.13),(9.14) и значение элементов ориентирования , после разложения тригонометрических функций в ряд с сохранением членов первого порядка малости запишем:

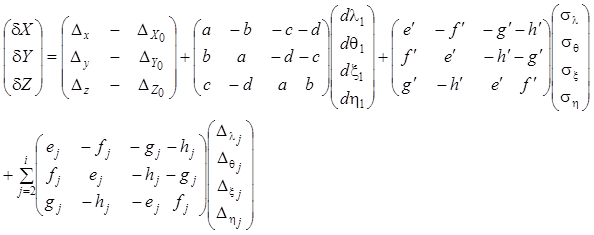   (9.15)

где , ,  и , ,  - погрешности измерения координат соответственной точки -ой модели и точки исходной модели, принятой за начало координат.

Коэффициенты , , ,… вычисляются из выражений:

,         ,         ,

,            .           ,

,            ,          ,

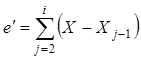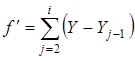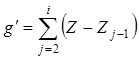Ошибки записаны в масштабе построения маршрутной сети.

Уравнение (9.15) характеризуют деформацию координат точек маршрутной сети, вызванную совместным действием погрешностей определения элементов ориентирования исходной модели и систематическими и случайными  ошибками ее построения.