Математическое моделирование на ЭВМ, страница 9

Возможно составление единой целевой функции, куда включаются разные критерии, но каждый со своим весом.

Многокритериальные задачи решают с привлечением оценок экспертных. Что лучше: быть бедным, но здоровым, или богатым, но больным задача - не для математических методов.

Различают оптимизационные модели двух видов – с ограничениями и без ограничений.

В задачах без ограничений выполняется поиск экстремума целевой функции без наложения каких-либо ограничений на область изменения переменных.

Задачи с ограничениями - это задачи поиска экстремумов функций многих переменных с ограничениями на область изменения переменных. Раздел математики, изучающий задачи с ограничениями называется математическим программированием. Математическое программирование, в свою очередь делится на ряд разделов. Назовем некоторые из них:

-  линейное программирование – целевая функция и связи между параметрами линейные;

-  выпуклое или нелинейное программирование – целевая функция или связи между параметрами нелинейные;

-  дискретное программирование – переменные изменяются дискретно, частный случай – целочисленное программирование, когда все переменные – целые числа;

-  динамическое программирование – целевая функция или связи между параметрами являются непостоянными и в ходе решения задачи изменяются;

-  стохастическое программирование – модель носит вероятностный характер, используется при переменчивости или недостоверности используемой моделью информации.

Математическое программирование – развивающееся направление, появляются новые типы задач и методов их решения такие, как программирование параметрическое, блочное, сетевое, булевское, комбинаторное.

4.2. Геодезические примеры оптимизационных задач

1.Уравнивание геодезической сети.

При обработке геодезических измерений вследствие погрешностей измерений и благодаря их избыточности обнаруживается противоречивость, несовместность результатов измерений, которую устраняют путем уравнивания сети.  При уравнивании ищут поправки v₁, v₂, … , v_n к результатам измерений такие, чтобы целевая функция [pv²] имела минимальное значение.

Это - задача на поиск экстремума без ограничений.

2.Рихтовка рельсовой нити.

Выполнена съемка монорельсового пути с целью его выпрямления. При этом в точках  измерены ординаты . Необходимо рассчитать величину рихтовок для выпрямления кривой рельсовой нити.

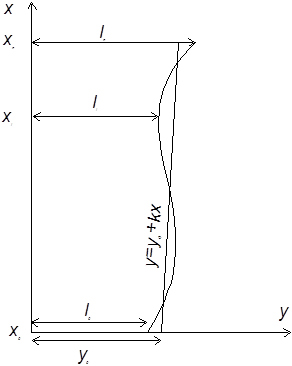
Напишем для выпрямленного пути уравнение . Тогда для рихтовок в точках с номерами i =  0, 1, … , n, то есть для смещений v_i пути в прямолинейное положение запишем

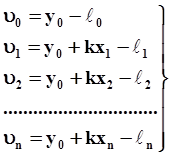          (4.1)

Выбором параметров y₀ и k определяется величина всех рихтовок v_i. Выберем такие параметры y₀ и k, чтобы сумма квадратов рихтовок была минимальной.

Таким образом, математическая модель задачи включает целевую функцию [v²] = min и систему уравнений (4.1).

3.Рихтовка рельсовой нити с учетом ограничений.

Выполнена съемка монорельсового пути с целью его выпрямления. При его рихтовке необходимо учесть наличие вблизи пути препятствий, ограничивающих величину смещения рельсов. Иными словами, на величину рихтовок наложены ограничения.

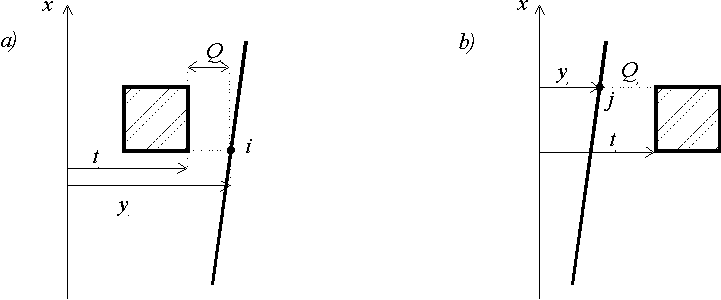
При наличии препятствия слева (см. рис а) на положение выправленного рельса наложено ограничение . Запишем это неравенство так:

       (4.2)

При наличии препятствия справа (см. рис b) на положение выправленного рельса наложено ограничение . Запишем это неравенство так:

       (4.3)

В результате получаем систему равенств (4.1) и неравенств – ограничений вида (4.2) и (4.3).

Возникает задача математического программирования, в которой требуется минимизировать рихтовки с учетом ограничений.

Если целевая функция имеет вид , или иначе - , то задачу решают методом линейного программирования.

Если целевая функция имеет вид , то задачу решают методом квадратического программирования.

Контрольные вопросы

12.  Особенности оптимизационной модели.

13.  Что такое метод экспертных оценок, зачем он нужен?

14.  Что такое задача линейного программирования (ЗЛП)?