Профиль трассы: каждому пикету отвечает своя отметка.
Оскулирующая орбита спутника Земли, модель реальной, фактической орбиты – каждому моменту времени соответствуют вполне определенные пространственные координаты и вектор скорости спутника.
2.2. Математическая модель геодезической сети.
Для построения геодезической сети измеряют элементы сети (углы, расстояния) и, зная координаты исходных пунктов, вычисляют координаты определяемых пунктов. При этом результаты выполненных измерений уравнивают. Метод уравнивания зависит от гипотезы о законе распределения погрешностей измерений. Гипотезе нормального распределения отвечает уравнивание методом наименьших квадратов. Гипотезе распределения Лапласа отвечает уравнивание методом наименьших модулей. В зависимости от выбранной гипотезы, обработка выполняется по разным алгоритмам и приводит к разным значениям оценок искомых координат определяемых пунктов. Реальный, фактический закон распределения погрешностей неизвестен и конечно отличается от предполагаемого идеализированного закона. Поэтому, выбирая ту или другую гипотезу, мы принимаем более адекватную, с нашей точки зрения, математическую модель. Но в любом случае получаем детерминированную модель. На одни и те же значения входных параметров она отвечает вполне определенными выходными параметрами, что и используется, например, при контроле правильности вычислений выполнением их «в две руки».
Схема детерминированной математической модели геодезической сети:
Вход Модель Выход
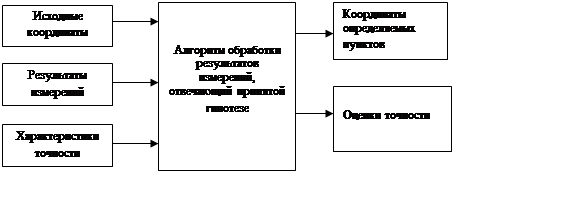 |
Входными параметрами являются результаты измерений, координаты исходных пунктов, характеристики точности измерений.
Содержание модели – алгоритм обработки результатов измерений.
Выходные параметры – координаты определяемых пунктов, оценки их точности.
Адекватность модели определяется корректностью алгоритмов, в частности – учетом необходимых поправок к результатам измерений, верностью принятой гипотезы, правильностью методики уравнивания.
2.3. Нелинейные модели геодезической сети.
Связь между входными и выходными параметрами геодезической сети описывается уравнениями связей. Эти уравнения, как правило, имеют нелинейный вид. Рассмотрим основные уравнения связей, существующие в плановой геодезической сети при применении плоских координат.
Уравнение связи между измеренными элементами ![]() и
координатами пунктов
и
координатами пунктов ![]() запишем в общем виде
запишем в общем виде
![]() (2.1)
(2.1)
Так, расстояние S между
пунктами 1 и 2 и их координаты ![]() связаны уравнением
связаны уравнением
![]() (2.2)
(2.2)
Дирекционный угол направления с пункта 1 на пункт 2 с координатами пунктов связан уравнением
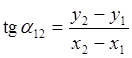 (2.3)
(2.3)
Горизонтальный угол на пункте 1 между направлениями на пункты. 2 и 3 с координатами трех пунктов связан уравнением
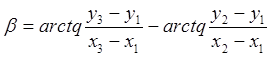 (2.4)
(2.4)
Уравнения связи (2.2), (2.3), (2.4) представляют собой математические модели измеренных элементов.
Система таких уравнений, связывающих всю совокупность известных координат исходных пунктов и измеренных элементов с неизвестными координатами определяемых пунктов, представляет собой детерминированную нелинейную математическую модель геодезической сети. Решением системы уравнений связи находят координаты определяемых пунктов.
Однако прямое решение системы уравнений связи применяется только в очень простых сетях, какими являются, например, геодезические засечки (прямая, обратная, линейная, комбинированная).
2.4. Линейные модели геодезической сети.
Линейная зависимость одной величины от другой означает пропорциональность их приращений.
В линейных уравнениях все переменные участвуют в первой степени. Решение систем линейных уравнений значительно проще, чем нелинейных. Для упрощения нелинейную модель, представленную уравнениями связей, линеаризуют.
Зададимся приближенными координатами ![]() пунктов.
пунктов.
Разложим правую сторону уравнения связи (2.1) в ряд
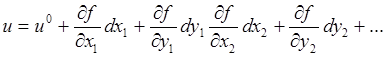
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.