Математическое моделирование на ЭВМ, страница 7

Вычислив дисперсии – оценить рассеяние оценок

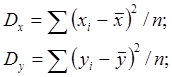
их корреляционные моменты

средние квадратические отклонения

;   .

Применение стохастической модели геодезической сети позволяет:

- рассчитать точность нужных элементов сети;

- сравнить достоинства разных алгоритмов, в том числе нестрогих и таких, для которых неизвестны формулы оценки точности;

- сравнить варианты схемы сети;

- получить такую оценку, которая недоступна другим методам - отклонения от «истинного».

3.2. Моделирование ошибок измерений.

Моделью ошибок измерений служат случайные числа, подчиненные тому же закону распределения, что и ошибки.

3.2.1. Моделирование равномерно распределенных погрешностей.

Основные сведения о равномерном распределении

Равномерно распределенные погрешности встречаются, но редко. Но равномерно распределенные на заданном интервале числа широко используются при моделировании погрешностей с иными распределениями. Поэтому рассмотрим методы создания равномерно распределенных случайных чисел.

Случайная величина  равномерно распределена на интервале (-а, +а), если любое ее значение из этого интервала равновероятно (см. рис.).

Сказанное означает постоянство на заданном интервале плотности вероятности.

Следовательно, функция плотности вероятности имеет вид:

х

-а

Р=1

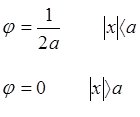
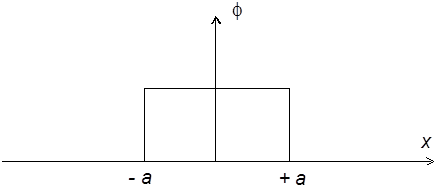
Поэтому функция распределения, называемая еще интегральной функцией распределения и указывающая вероятность непревышения величины х, имеет вид:

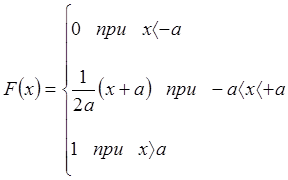
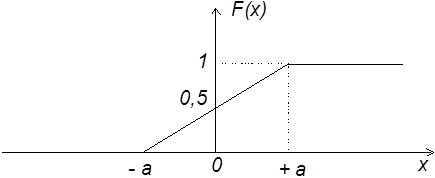
Определим дисперсию равномерно распределенной случайной величины

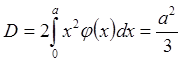
Моделирование равномерно распределенных чисел

Во всех ЭВМ предусмотрена возможность получения равномерно распределенных случайных чисел. Существует два подхода.

1. Физический. В конструкцию ЭВМ включают специальный датчик случайных чисел. Датчики бывают радиоактивные и радиошумовые.

2. Программный. Случайные числа вычисляют, используя рекуррентные алгоритмы. Каждое следующее число вычисляют, используя предыдущие. Например, взяв два произвольных числа x_i-1 и x_i, следующее число x_i+1 вычисляют, взяв средние цифры из произведения x_i-1´x_i.

В персональных компьютерах пользуются программным способом.

В языке Паскаль предусмотрены две команды. Команда Randomise –  запускает датчик случайных чисел. Команда x:= Random(Q) – присваивает переменной х случайное значение из интервала 0Q, то есть случайное число с математическим ожиданием  и дисперсией  , где Q – целое.

Если хотим получить числа в интервале (-0,5  +0,5), то преобразуем выданные Паскалем случайные числа х по формуле

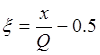, где х – равномерно распределено на интервале (0  Q).

Дисперсия чисел  будет равна

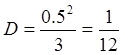
В языке Бейсик для получения равномерно распределенных чисел предусмотрена команда Random. То есть в этом случае Q = 1.

3.2.2. Моделирование нормально распределенных погрешностей.

Нормальное распределение (распределение Гаусса) характеризуется формулами: плотность вероятности - 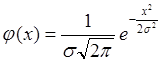, функция распределения - 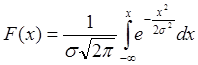, дисперсия - D = s². 

График плотности вероятности j(х)	График функции распределения F(x)

Из теории вероятностей известно, что сумма одинаково распределенных случайных чисел  распределена практически нормально. Это положение, доказанное Ляпуновым, практически справедливо уже при n = 5.

Воспользуемся числами x_i (i = 1, 2, … , n), распределенными равномерно. Сложив их, получим случайное число h

, где число h распределено нормально.

При этом его дисперсия будет равна:

Учитывая, что 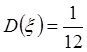, возьмем 12 таких чисел. Получим

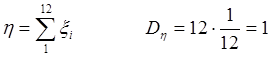
Т.е. суммируя по 12 равномерно распределенных на интервале –0,5   +0,5 чисел, получаем нормально распределенные числа с дисперсией = 1.

Для получения чисел с дисперсией, равной  надо числа  умножить на стандарт

3.2.3. Моделирование погрешностей с любым заданным распределением.

Пусть требуется создать выборку случайных чисел с плотностью вероятности j(х) и соответственно функцией распределения