Математическое моделирование на ЭВМ, страница 5

Решив систему нормальных уравнений, найдем поправки 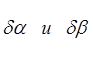 к параметрам a₀ и b₀ и оценим точность полученной эмпирической формулы – ее среднее квадратическое отклонение от экспериментальных точек 

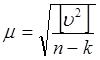
где n – число точек и - число параметров

Пример. Выполнено 30 ежемесячных циклов наблюдений за осадками сооружения. Результаты изменения высоты одной из деформационных марок приведены в таблице. Для прогнозирования дальнейших осадок составим модель осадок этой марки в виде эмпирической формулы.

Номер месяца i	Величина осадки z, мм	Номер месяца i	Величина осадки z, мм	Номер месяца i	Величина осадки z, мм
1 2 3 4 5 6 7 8 9 10	148.244 134.372 123.397 110.701 97.909 95.818 86.93 82.114 81.78 69.964	11 12 13 14 15 16 17 18 19 20	64.926 59.185 54.602 49.247 38.371 39.162 32.517 35.267 28.957 24.552	21 22 23 24 25 26 27 28 29 30	21.903 20.595 22.942 17.949 17.657 20.857 11.627 13.213 16.499 14.600

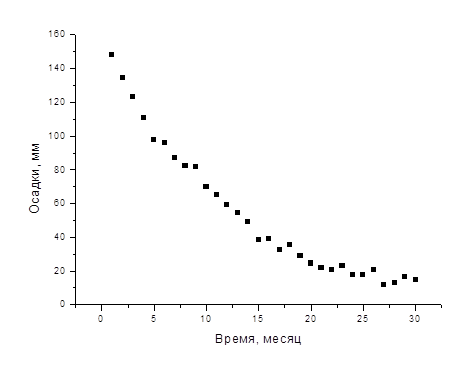
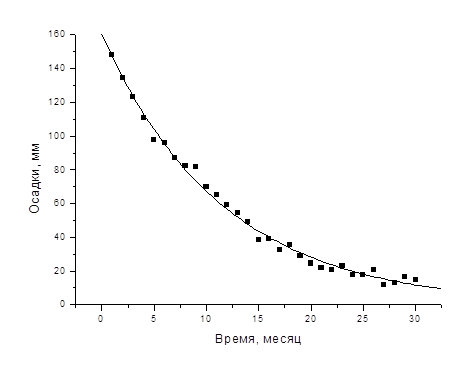
По данным таблицы составлен график изменения осадок. Для моделирования процесса осадок выбрана формула следующего вида

                                 (2.20)

где х – номер месяца.

Из принятой формулы следует, что при x = 1 имеем y = a.. С другой стороны, согласно данным таблицы значению х = 1 соответствует у₀ =  148,24 мм. Поэтому за приближенное значение a можем принять a₀ = 148,244.

Для определения приближенного значения  используем одну из точек, удаленных от начальной. Например, возьмем точку x₂₅ = 25; у₂₅ = 17,657 мм. Тогда согласно (2.20) получим

17,657 = 148,244 е ^-24b

или

 =  0,089.

Коэффициенты и свободные члены уравнений поправок вычислим по формулам: ;    ;    .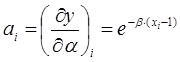

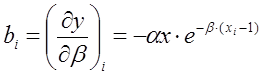(i = 1, 2, … , 30)

Коэффициенты и свободные члены нормальных уравнений:

[aa] = 6,103;   [ab] = - 0,005;  [bb] = 8,447×10⁶;  [al] = -2,994;  [bl] = 1,064×10⁴.

Поправки к приближенным параметрам: da  =  -0,915; db = -0,003.

Исправленные параметры: a₀ + da  = 146,784; b₀ + db  = 0,087.

Среднее квадратическое отклонение m = 3,3 мм.

Ниже на рисунке кроме экспериментальных точек  показана кривая, иллюстрирующая модель поведения осадок, описываемую формулой

y = 146,784×exp[-0,087×(x - 1)].

Подставляя в полученную формулу время x, можно предсказывать вероятное поведение осадок в будущем.

Составление эмпирических формул существенно упрощается при использовании специального программного обеспечения. Так, в системе MATHCAD для построения экспоненты, наиболее соответствующей имеющимся числовым данным, имеется функция expfit(vx, vy, vg), которая выдает вектор (abc) параметров формулы . Исходными данными для вычисления коэффициентов служат векторы vх и vу экспериментальных данных, а также вектор приближенных значений коэффициентов a, b и с. В нашем примере vx это - вектор номеров месяцев x_i, вектор vy - вектор наблюденных осадок z_i, а vg - вектор приближенных значений параметров формулы, например (148  -0.09  0). Для этого примера функция expfit выдала вектор (161.269  -0.084 1.617). Кривая, построенная по этим данным, практически неотличима от приведенной выше на рисунке. 

В системе MATHCAD кроме экспоненты предусмотрена возможность построения иных функций, которые могут в разных случаях более правильно отражать связи между экспериментальными данными. В таблице приведены некоторые примеры таких функций.