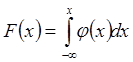Математическое моделирование на ЭВМ, страница 8

, где F(x) = P – вероятность непревышения случайным числом значения х.

График функции распределения F(x) -

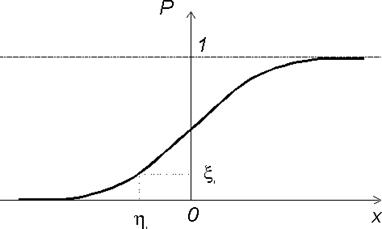
Вероятность попадания числа в интервал Dx равна соответствующему отрезку  DP на оси вероятностей Р. Равенство разных отрезков DP означает равную вероятность попадания в соответствующие интервалы Dx.

Переходя к бесконечно малым величинам будем вместо отрезков иметь точки и сказанное выше будет означать, что всякая точка на оси Р в интервале (0; 1) равновероятна. И каждой такой точке будет соответствовать точка на кривой и точка на оси х.

Следовательно, для формирования выборки таких случайных чисел h_i, появление которых при заданном распределении было бы равновероятным, следует поступить так.

Выбираем случайные числа x_i, равномерно распределенные на оси Р в интервале (0; 1). Каждому такому числу соответствует распределенное по закону  число h_i (см. рисунок). Для численного определения числа h_i по известному числу x_i надо решить интегральное уравнение

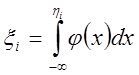
где - заданная функция плотности распределения;  - случайные равномерно  распределенные числа из интервала (0;1); h_i - решение интегрального уравнения – число с распределением

3.2.4. Моделирование погрешностей с заданным распределением средствами системы MathCad.

Для моделирования погрешностей с нормальным распределением применяется функция rnorm(n, m, s), которая возвращает вектор, состоящий из n случайных чисел с  математическим ожиданием m и средним квадратическим отклонением s.

Для моделирования погрешностей с экспоненциальным распределением

применяется функция rexp(n, r), которая возвращает вектор, состоящий из n случайных чисел с  параметром экспоненциального распределения r.

Для моделирования чисел с равномерным распределением на интервале (а, b)

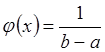
применяется функция runif(n, a, b), которая возвращает вектор, состоящий из n случайных чисел, равномерно распределенных на интервале (а, b).

Контрольные вопросы

7.  Содержание стохастической модели геодезической сети.

8.  Как оценивают точность определяемых параметров в стохастической модели геодезической сети?

9.  Что обычно служит моделью ошибок измерений?

10.  Как моделируют нормально распределенные ошибки измерений?

11.  Как моделируют иначе распределенные ошибки измерений?

4. Оптимизационные модели.

4.1. Понятие об оптимизационных моделях

Рассмотренные ранее модели носят описательный характер. Они описывают поведение объекта в зависимости от изменений входных параметров. Такие модели называют дескриптивными (описательными).

Изменяя входные параметры модели, и наблюдая за изменениями выходных, можем выбрать такие входные параметры, которые лучше, ближе приводят выходные параметры к цели.

Например: В модели геодезической сети (детерминированной или стохастической), изменяя состав и точность угловых и линейных измерений, получаем разную точность координат пунктов  на выходе модели. Но уверенности, что нами найден самый лучший вариант – нет.

Для отыскания наилучшего решения служат оптимизационные модели.

С

Чтобы построить оптимизационную модель, необходимо установить критерий оптимальности – целевую функцию.

Примеры целевых функций.

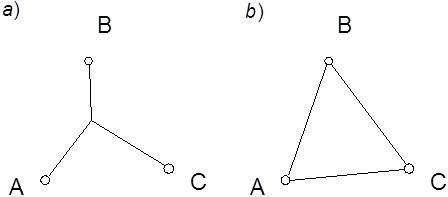
Пример 1. Требуется соединить дорогами три пункта: А, В и С (см. рис.). Минимизация стоимости строительства приводит к варианту а. Минимизация времени проезда – к варианту б.

Пример 2. Уравнивание геодезической сети методом наименьших квадратов. Целевая функция – [v²] = min. Можно уравнивать методом наименьших модулей. Тогда целевая функция имеет вид [|v|] = min.

Важно указать, что математические методы решают задачи с единственным критерием оптимальности.

Например, можно ставить задачу – выполнить съемку максимальной площади при заданном объеме ресурсов. Или задачу достижения минимальных затрат при заданной площади съемки. В первом случае целевая функция – максимальная площадь съемки, во втором – минимум затрат.