Математическое моделирование на ЭВМ, страница 6

Кроме компьютерных программ, использующих при подборе эмпирических формул метод наименьших квадратов, существуют программы, использующие робастные методы, которые рекомендуются при наличии грубых ошибок наблюдений. К ним относятся методы составления таких эмпирических формул, от которых отклонения экспериментальных точек отвечают таким критериям, как минимум суммы отклонений точек от кривой, минимум дисперсии в предположении, что рассеяние опытных точек подчинено распределению Лоренца, минимум дисперсии в предположении, что рассеяние опытных точек подчинено распределению Пирсона и др.

Контрольные вопросы

1.  Какого типа модель применяют при традиционной технологии уравнивания геодезической сети?

2.  Что такое линеаризация модели и зачем она?

3.  Модель ошибок измерений в геодезической сети представлена системой n параметрических уравнений поправок. Как отражается гипотеза о преобладании систематических ошибок над случайными?

4.  Модель ошибок измерений в геодезической сети представлена системой n параметрических уравнений поправок. Как отражается гипотеза о преобладании случайных ошибок над систематическими?

5.  Модель ошибок измерений в геодезической сети представлена системой n параметрических уравнений поправок. Как отражается гипотеза о наличии систематических ошибок одного порядка со случайными?

6.  Как оценивают точность определяемых параметров в детерминированной модели геодезической сети?

3. Стохатические модели.

Модель, отвечающая на одни и те же входные параметры в разных случаях разными входными сигналами, носящими случайный характер, называется недетерминированной или стохастической.

Модель, отражающая процесс измерений с учетом случайного характера погрешностей измерений, должна быть стохастической.

3.1. Стохастическая модель геодезической сети.

Задачей моделирования является анализ свойств некоторого алгоритма обработки результатов измерений, выполненных с целью создания геодезической сети. Требуется выявить свойства оценок, получаемых с помощью испытуемого алгоритма.

Испытания алгоритма выполняются на конкретной сети.

Схема модели показана на рисунке.

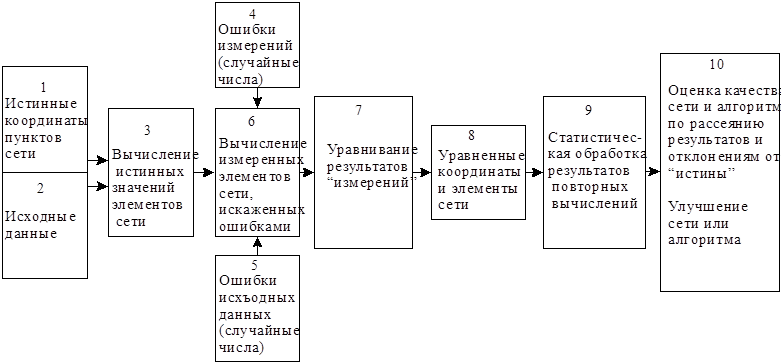
Входными параметрами модели являются истинные координаты пунктов сети (исходных и определяемых) и список измеряемых элементов. Эти параметры не изменяются от опыта к опыту. К числу исходных данных могут быть отнесены и иные априори задаваемые величины, такие, например, как параметры, используемые при вычислении поправок к результатам измерений. Истинные значения исходных данных из блоков 1 и 2 используются для вычисления истинных значений измеряемых элементов сети элементов: углов, длин линий и пр. (блок 3). 

Для получения модели измеренных величин истинные их значения искажаются моделью погрешностей измерений и исходных данных (блок 6). Погрешности моделируются как случайные числа с заданным распределением (блоки 4 и 5). В результате ввода случайных погрешностей на выходе блока 6 при каждом новом опыте будем получать новые случайные числа – модель результатов измерений. 

Выполнив уравнивание результатов измерений с применением испытуемого алгоритма (блок 7), получаем уравненные координаты пунктов и уравненные элементы сети (блок 8).

Вычисления и выдачу результатов повторяют многократно, получая каждый раз новые случайные значения уравненных координат и элементов сети. 

В блоке 9 происходит накопление результатов вычислений и их статистическая обработка.

По результатам статистической обработки принимают решения о необходимости внесения изменений в испытуемый алгоритм или схему сети (блок 10).

Перед статистической обработкой результатов многократного уравнивания сети могут быть поставлены различные задачи. Например, имея уравненные координаты некоторого пункта где n - число опытов, можем вычислить их средние значения :

;   .

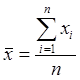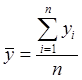Вычислив отклонения средних от известных истинных значений, можем оценить несмещённость оценок, доставляемых испытуемым алгоритмом

  

где х_ист, у_ист – истинные координаты.