Математическое моделирование на ЭВМ, страница 3

Перепишем полученное линейное уравнение, обозначив частные производные буквами a, b, …, и перейдя от дифференциалов dx, dy к поправкам  dx, dy.

, где , причем u^изм – измеренное значение элемента сети u, а du - поправка к результату измерения.

Получили уравнение поправок:

Перепишем его в более привычном виде

               (2.5)

Наличие в сети измеренных элементов приводит к системе уравнений поправок

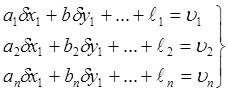       (2.6)

В геодезических сетях число измерений всегда больше числа неизвестных.

Из-за ошибок измерений система уравнений (2.6) оказывается несовместной и решают ее методом наименьших квадратов.

То есть, вместо невозможного

v_i = 0    (i = 1, 2, …,n)

добиваются минимума целевой функции

[v²] = min.

При неравноточных измерениях веса p_i уравнений неодинаковы и целевой функцией является

[pv²] = min.

Производные 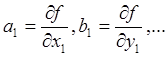могут быть вычислены численным методом, но чаще их определяют по известным формулам.

Примеры.

Уравнение поправок для измеренного расстояния.

Напишем уравнение связи для расстояния между пунктами i и j.

s² = (x_j –x_i)² + (y_j – y_i)².

Продифференцируем его по всем переменным

2s ds = 2 (x_j –x_i) (dx_j – dx_i) + 2 (y_j – y_i) (dy_j – dy_i).

Перейдем к поправкам и учтем, что Dx / s = cosaи Dy / s = sina. Получим

cosa_ji dx_i + sina_ji dy_i + cosa_ij dx_j + sina_ij dy_j = ds .

Учтем, что

ds = s – s⁰ = s^изм + v_s – s⁰ , и получим окончательно

cosa_ji dx_i + sina_ji dy_i + cosa_ij dx_j + sina_ij dy_j + (s^изм - s⁰) = v_s .        (2.7)

Уравнение поправок для измеренного дирекционного угла.

Напишем уравнение связи

.

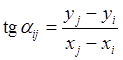Дифференцируя его, напишем

cosa_ij (x_j - x_i) da + sina_ij dx_j - sina_ij dx_i = - sina_ij (y_j - y_i)da + cosa_ijdy_j

-cosa_ijdy_i.

Разделим полученное уравнение на расстояние s и учтем, что

cosa_ij (x_j - x_i)  + sina_ij (y_j - y_i) = s.

Получим

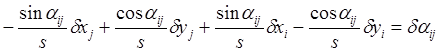                    (2.8)

Учтем, что

da_ij = a_ij - a_ij⁰ =  a_ij^изм + v_a- a_ij⁰ , и получим окончательно

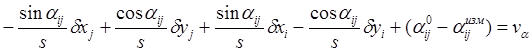
Уравнение поправок для измеренного горизонтального направления.

Пусть на некотором пункте измерены горизонтальные направления. Дирекционный угол любого из них равен

a = b + R,                                                                                         (2.9)

где - направление, отсчитываемое от начального направления, дирекционный угол которого равен R.

Для приближенных значений тех же элементов, вычисленных по приближенным координатам, напишем

a⁰ = b ⁰+ R⁰,                                                                                      (2.10)

Заменяя же в (2.9) истинные элементы уравненными, напишем

a⁰ + da = b^изм + v_b + R⁰ + dR,                                                          (2.11)

Вычтя (2.10) из (2.11), получаем

da = dR - (b ⁰ - b^изм) + v_b.

Заменим теперь в (2.8) поправку к дирекционному углу da  последним выражением. Получим уравнение поправок горизонтального направления.

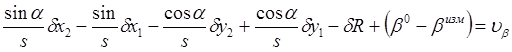
2.5. Зависимость математической модели геодезической сети от гипотезы о характере ошибок измерений.

Чтобы математическая модель геодезической сети была адекватна объекту, адекватна реальной, созданной с помощью измерений сети, построенная модель должна верно отражать все существенные стороны выполненных измерений. Покажем, что существенными являются не только значения измеренных элементов, но и характер погрешностей измерений.

Рассмотрим это на примере определения координат пункта линейной засечкой с 4-х пунктов (см. рис.).

Исходными данными являются:

-  координаты пунктов: 1, 2, 3, 4;

-  результаты измерения расстояний:

Зададимся приближенными координатами пункта Р и построим математическую модель в виде системы уравнений поправок.

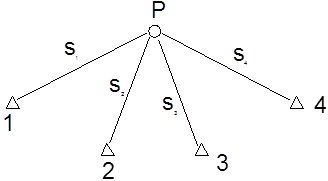
Оказывается, модель неоднозначна и зависит от гипотезы о характере ошибок измерений.

Рассмотрим варианты, соответствующие разным гипотезам.

Гипотеза 1. Предполагаем, что результаты измерения расстояний s₁, s₂, s₃, s₄ содержат только случайные ошибки. Уравнения поправок имеют вид:

           (i = 1, 2, 3, 4)

здесь - поправки к рензультатам измерений, призванные устранить, а точнее – ослабить, случайные ошибки.