Перепишем систему уравнений поправок, обозначив для
краткости коэффициенты - ![]() параметры -
параметры - ![]() свободные члены
свободные члены ![]() :
:
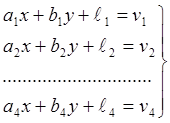 (2.12)
(2.12)
Решая систему уравнений поправок методом наименьших
квадратов, найдем поправки к приближенным координатам x
и у, соответствующие минимуму целевой функции ![]() .
.
Гипотеза 2. Предположим, что результаты измерения расстояний s1, s2, s3, s4 кроме случайных ошибок содержат значительную систематическую погрешность. Тогда кроме поправок v1, v2, v3, v4, направленных на ослабление случайных погрешностей должна быть введена общая для всех измерений поправка d, для компенсации общей систематической ошибки. Уравнения поправок принимают вид:
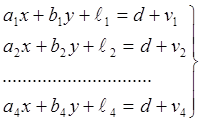 (2.13)
(2.13)
или
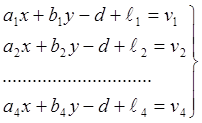 (2.14)
(2.14)
Теперь определяемых параметров три – х, у
и d. Решая систему уравнений поправок методом наименьших квадратов,
минимизируем целевую функцию ![]() . На величину поправки d при этом никаких
ограничений не накладывается, в чем проявляется гипотеза о возможности
значительной систематической ошибки, превышающей случайные.
. На величину поправки d при этом никаких
ограничений не накладывается, в чем проявляется гипотеза о возможности
значительной систематической ошибки, превышающей случайные.
Гипотеза 3. Выполнено компанирование дальномера. Систематическая ошибка устранена с некоторой, общей для всех измерений погрешностью. Теперь модель (2.12) не адекватна условиям задачи, так как предполагает полное отсутствие общей ошибки.
Модель (2.14) тоже не адекватна – она предполагает наличие доминирующей систематической ошибки.
Согласно гипотезе 3 модель надо записать так:
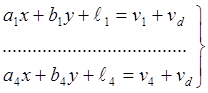 (2.15)
(2.15)
и минимизировать сумму
![]()
Для удобства решения задачи перепишем (2.15) иначе, добавив к системе уравнений тождество:
![]()
Запишем
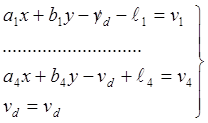 (2.16)
(2.16)
В левой части уравнений – три определяемых параметра х,
у и vd. Решая систему уравнений поправок методом наименьших
квадратов, найдем поправки x и у, соответствующие минимуму целевой функции ![]() , где в
список минимизируемых поправок включена и поправка vd.
, где в
список минимизируемых поправок включена и поправка vd.
2.6. Эмпирические формулы.
В практике нередки случаи, когда в результате наблюдений за поведением некоторого объекта получают ряд значений двух (или более) параметров, и требуется сформулировать математическую модель, отражающую связь между этими параметрами.
Например, сравнивая результаты измерения расстояний оптическим дальномером с эталонными значениями тех же расстояний, можем составить математическую модель ошибок измерений в виде эмпирической формулы и использовать эту формулу в дальнейшем для вычисления поправок в результаты измерений.
Другой пример. Наблюдая за осадками возведенного сооружения, стремятся сформулировать зависимость осадок от времени, построив модель процесса в виде формулы, которая позволяла бы оценить темп затухания процесса, прогнозировать величину осадок на будущее.
Рассмотрим порядок составления эмпирической формулы.
Пусть в результате экспериментов получен ряд значений двух переменных – х и у.
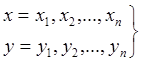 (2.17)
(2.17)
Необходимо подобрать формулу, отражающую связь между переменными x и y. Действия по подбору формулы выполняют в следующем порядке.
1. Точки с координатами xi, yi наносят на график. Рассматривая график, устанавливают примерный вид кривой, проходящей через нанесенные точки, обнаруживают и отбрасывают точки сильно от нее отклоняющиеся, как содержащие грубые ошибки.
2. Исходя из теоретических соображений и вида кривой, подбирают вид эмпирической формулы. Чем более обоснована формула теоретически, тем создаваемая модель будет адекватнее.
Запишем выбранную формулу в общем виде
![]() (2.18)
(2.18)
Задача состоит в том, чтобы найти наилучшие значения
параметров ![]()
3. Назначают некоторые приближенные значения ![]() и получают
приближенную формулу
и получают
приближенную формулу
![]() (2.19)
(2.19)
4.
Улучшают параметры ![]() поправками
поправками 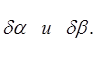 Для вычисления поправок da и db, разложим (2.18) в ряд:
Для вычисления поправок da и db, разложим (2.18) в ряд:
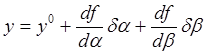
Обозначим
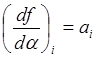 ;
; 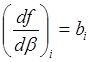 ;
; ![]()
![]()
где
значения ![]() -
вычислены по приближенной формуле (2.19) по значениям
-
вычислены по приближенной формуле (2.19) по значениям 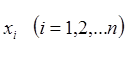
Получаем систему линейных уравнений поправок
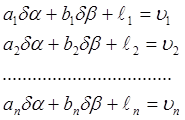
Для решения системы уравнений поправок методом наименьших квадратов, составим нормальные уравнения
[aa] da + [ab] db + [al] = 0
[ab] da + [bb] db + [bl] = 0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.