5.1. Задача линейного программирования (ЗЛП)
Линейная функция z = c1x1 + c2x2 + … + cnxn в зависимости от значений переменных x1, x2, … , xn может принимать сколь угодно большие или малые значения. Поэтому нельзя ставить задачу поиска экстремума линейной целевой функции без наложения каких-либо ограничений на область изменения переменных. Если же существуют такие ограничения, то в замкнутой этими ограничениями области экстремумы функции z существуют.
Если целевая функция z и ограничения на область изменения переменных x1, x2, … , xn представлены линейными выражениями, то задача отыскания оптимума целевой функции называется задачей линейного программирования (ЗЛП).
Задачи линейного программирования встречаются в самых разных областях науки и техники, в том числе и в геодезии. Но первые применения они нашли в экономических расчетах, поэтому задачу линейного программирования принято излагать в экономических терминах. Кроме того, такое изложение обладает наглядностью.
Пусть имеется m видов сырья в следующих количествах: b1, b2,…, bm .
Из этого сырья можно изготовить n видов продуктов.
Количество i-го вида сырья (i = 1, 2, … , m), необходимого для получения единицы j-го продукта (j = 1, 2, … , n) обозначим аij.
Количество j- го продукта обозначим хj.
Цена единицы каждого из продуктов соответственно равна с1, с2,…, сn.
Цена j-го продукта равна сj хj.
Суммарная цена всей продукции равна 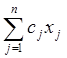 . Нужен ее
максимум.
. Нужен ее
максимум.
Таким образом, математическая модель задачи приобретает вид:
- целевая функция
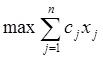 ;
;
- условия-ограничения:
1. ![]() j = 1, 2, … , n; (5.1)
j = 1, 2, … , n; (5.1)
2. 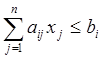 i = 1, 2, … , m. (5.2)
i = 1, 2, … , m. (5.2)
Всякий набор параметров ![]() ,
удовлетворяющий условиям (5.1) и (5.2), называется допустимым планом
(стратегией, управлением). Допустимый план, обеспечивающий максимум целевой
функции называется оптимальным планом.
,
удовлетворяющий условиям (5.1) и (5.2), называется допустимым планом
(стратегией, управлением). Допустимый план, обеспечивающий максимум целевой
функции называется оптимальным планом.
5.2. Геометрическая интерпретация задачи линейного программирования
Рассмотрим задачу линейного программирования в случае двух переменных. Такое число переменных позволяет геометрическую интерпретацию на плоскости, а также графическое решение задачи. После рассмотрения задачи в двухмерном пространстве понятнее становятся решения в многомерном пространстве.
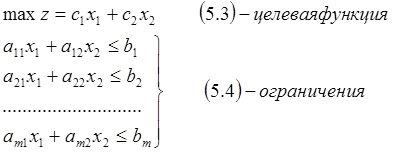
![]() (5.5)
(5.5)
Каждое из ограничений (5.4) и (5.5) задает полуплоскость возможных значений x1 и x2. Неравенства x1 ³ 0 и x2 ³ 0 ограничивают значения x1 и x2 первой четвертью. Неравенства ai1x1 + ai2x2 £ bi тоже делят плоскость на две части. Покажем это.
Рассмотрим прямую ai1x1 + ai2x2 = bi. Возьмем на ней какую либо точку. В этой точке равенство соблюдается. Если увеличим x1, то левая сторона равенства будет больше bi, что недопустимо. То есть, если левая сторона равенства больше bi, то мы оказываемся в области недопустимых значений x1. Если уменьшим x1, то левая сторона равенства будет меньше bi , что допустимо. То есть мы попадаем в область допустимых значений x1.
Несколько неравенств вместе ограничивают площадь, которую называют областью допустимых решений или иначе - областью допустимых планов.
Например, область допустимых решений может быть ограничена многоугольником А1, А2 … А5 (см. рис.).
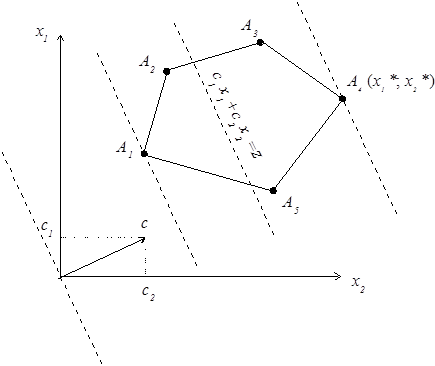
Рассмотрим целевую функцию
![]()
При фиксированном значении z это равенство есть уравнение прямой. При разных значениях z получим уравнения разных, параллельных друг другу прямых. Эти прямые называют линиями уровня целевой функции.
Если бы пространство было не двухмерным, а многомерным, то вместо линий уровня мы получили бы гиперплоскости уровня. В случае нелинейной целевой функции имели бы поверхности уровня.
Направление возрастания целевой функции характеризуется
производными: 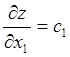 и
и 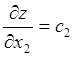 . Здесь
с1 и с2 – скорости возрастания целевой
функции Z по направлениям осей х1 и х2.
. Здесь
с1 и с2 – скорости возрастания целевой
функции Z по направлениям осей х1 и х2.
Вектор С = (с1; с2) называется градиентом целевой функции. Градиент указывает направление наискорейшего возрастания целевой функции z. Градиент перпендикулярен к линиям уровня.
Вектор, равный градиенту, но направленный в противоположную сторону указывает направление наискорейшего убывания целевой функции z.
Линейная целевая функция может иметь экстремум только
в ограниченной области. Если нет ограничений, то экстремум отсутствует.
Действительно, в случае двух параметров и целевой функции ![]() ее производные
ее производные 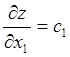 и
и 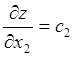 всегда не равны нулю. Значит, экстремумы
отсутствуют. При введении ограничений экстремум находится в одной из вершин ограничивающего
многоугольника.
всегда не равны нулю. Значит, экстремумы
отсутствуют. При введении ограничений экстремум находится в одной из вершин ограничивающего
многоугольника.
Возможные варианты иллюстрируются приведенными ниже рисунками, где обозначено Q - область допустимых решений, х* = (х1, х2) оптимальный план, параллельные линии, сплошные и штриховые, - линии уровня целевой функции. В варианте а - оптимальный план единственный (в точке х*); в варианте б - оптимальных планов бесконечно много (точки х*(1), х*(2), х*(3), …); в вариантах в и г - решения не существует, область допустимых решений не ограничена; в варианте д - область допустимых решений состоит из единственной точки, других решений не существует; в варианте е - система ограничений несовместна, область допустимых решений не существует, задача не имеет решения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.