Идея симплексного метода состоит в выполнении следующего плана действий, который иллюстрируется для случая двухмерного пространства рисунком, где сплошными линиями показаны границы области допустимых планов, а штриховыми – линии уровня целевой функции.
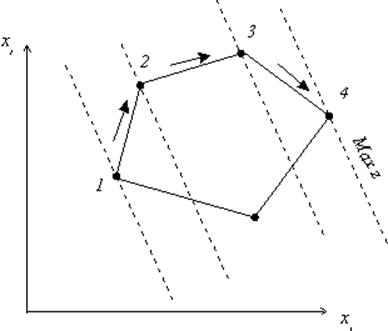
1. Система ограничений представлена в канонической форме и имеет предпочтительный вид.
Предпочтительным называется такой вид ограничений, когда каждое ограничение – равенство содержит такую переменную хi с коэффициентом +1, которая в других равенствах имеет коэффициент, равный 0.
Например,
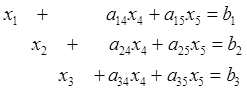
Предпочтительные переменные будем считать базисными. Остальные переменные – свободными. Свободные переменные приравняем нулю. Получаем следующий начальный опорный план:
x0 = (b1, b2, b3, 0, 0)
2. Система ограничений представлена неравенствами, имеющими неканонический вид:
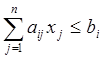 ;
; ![]() ;
;
![]() .
.
Систему ограничений приводят к каноническому виду, добавляя дополнительные переменные xn+i (i = 1, … , m). В итоге получим
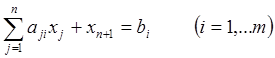
или, записав подробнее:
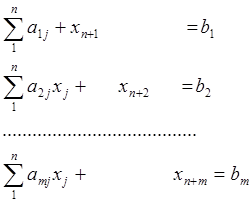
Система ограничений теперь имеет предпочтительный вид и позволяет составить начальный опорный план.
![]()
В целевую функцию дополнительные неизвестные входят с
коэффициентами ![]() .
.
Следовательно, начальное значение целевой функции, соответствующее начальному опорному плану, равно
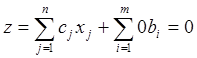 , то
есть прибыль z равна нулю. Все сырье (bi),
не принося прибыли, остается на складе.
, то
есть прибыль z равна нулю. Все сырье (bi),
не принося прибыли, остается на складе.
3. Система ограничений имеет вид
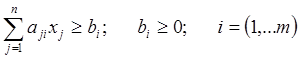
Система ограничений представлена не в канонической форме. Вычтем в каждом ограничении i дополнительное неизвестное xn+i (i = 1, … , m):
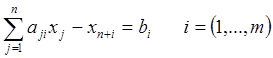
Система ограничений пробрела каноническую форму, однако не имеет предпочтительного вида и не позволяет составить начальный опорный план. Действительно, план (0, …, 0, -b1, -b2, …, -bm) не допустим, так как отрицательные значения xn+i не имеют смысла и недопустимы.
Надо продолжить преобразование системы ограничений и привести ее к предпочтительному виду, как показано ниже.
4. Система ограничений представлена в канонической форме, но не имеет предпочтительного вида.
Запишем целевую функцию -
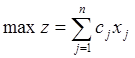 (6.1) и ограничения -
(6.1) и ограничения -
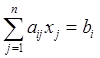 (i =
(i = ![]() )
(6.2)
)
(6.2)
xj ³ 0 (j = ![]() )
(6.3)
)
(6.3)
Чтобы придать системе ограничений (6.2) предпочтительный
вид прибавим к каждому из них искусственную переменную wi (i = ![]() ):
):
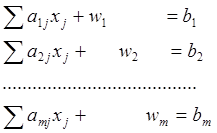 (6.4)
(6.4)
Введение искусственных переменных придает системе
ограничений предпочтительный вид, что позволяет построить из них искусственный
базис и составить начальный опорный план ![]() .
Однако в дальнейшем, в ходе применения симплекс-метода мы должны придти к
такому плану, который удовлетворяет ограничения (6.2), то есть свободные переменные
wi
должны стать равны нулю. Для этого целевой функции придают в случае поиска
максимума вид
.
Однако в дальнейшем, в ходе применения симплекс-метода мы должны придти к
такому плану, который удовлетворяет ограничения (6.2), то есть свободные переменные
wi
должны стать равны нулю. Для этого целевой функции придают в случае поиска
максимума вид
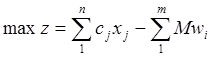 , а
при поиске минимума – вид
, а
при поиске минимума – вид
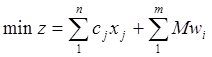 .
.
В обоих случаях экстремум целевой функции достигается, когда все wi равны нулю. Для повышения чувствительности этого критерия в функцию Z введен коэффициент М – большое положительное число.
Метод решения ЗЛП с введением искусственных переменных в литературе называют М – задачей или симплексным методом с искусственным базисом.
Любая ЗЛП может быть представлена в предпочтительном виде:
![]() ;
;
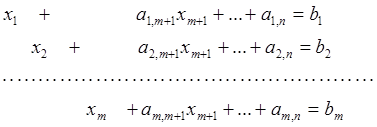
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.