Линейное программирование. Задача линейного программирования (ЗЛП), страница 5

где b_i ³ 0; x_j ³ 0   (i = ; j = ).

При этом начальный опорный план имеет вид :

Выразим базисные переменные х₁, х₁,…, х_m  через свободные переменные х_m+1, х_m+2,…, х_n.

Выражения для свободных переменных	Коэффициенты целевой функции
x1 = b1 - a1,m+1- … - a1,nxn	c1
x2 = b2 - a2,m+1- … - a2,nxn	c2
………………………………	…
xm = bm - am,m+1- … - am,nxn	cm
xm+1	cm+1
…	…
xn	cn

Подставим выражения для свободных переменных в целевую функцию z и сгруппируем подобные члены

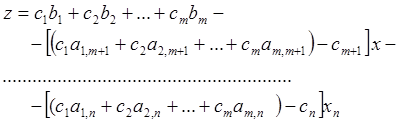
Перепишем полученное выражение так:

,                                                       (6.5)

где

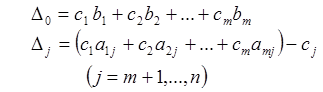
Другая, векторная форма записи этих же выражений

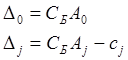
Чтобы опорный план  был оптимальным, иными словами - чтобы при  целевая функция z имела максимум, все  должны быть неотрицательными. Действительно, если в выражении (6.5) все D _j≥ 0, а x_m+1=0, x_m+2=0,…, x_n = 0, то целевая функция z имеет максимум, поскольку любое увеличение x_j (j > m) уменьшит значение z.

При этом .

Аналогично, для того чтобы целевая функция z имела минимум, все  должны быть неположительными.

Итак, признаки оптимальности опорного плана: для max z  - все D_j неотрицательны;

для min z  - все Dj неположительны.

6.4. Симплексная таблица

Исходные данные ЗЛП и результаты вычислений, реализующих симплексный метод, удобно размещать в виде таблицы, которую для краткости будем называть симплексной таблицей. Ниже приведена схема симплекс-таблицы.

БП	cБ	А0	х1	х2	…	xm	xm +1	…	xn
			с1	с2	…	cm	cm+1	…	сn
x1	с1	b 1	1	0	…	0	а1,m+1	…	a1,n
х2	с2	b 2	0	1	…	0	а2,m+1	…	a2,n
…	…	…	…	…	…	…	…	…	…
xm	cm	b m	0	0	…	1	am,m+1	…	am,n
Dj		∆0	0	0	…	0	∆m+1	…	∆n

В схеме использованы следующие обозначения.

БП – базисные переменные;

с_Б – коэффициенты целевой функции при базисных переменных;

А₀ – свободные члены ограничений - значения базисных переменных;

с_j и а_i,j  –  коэффициенты целевой функции и ограничений;

z_j- индексная строка, в которой: D₀ = с_БА₀ (скалярное произведение, которое равно значению целевой функции, т.к. свободные переменные равны нулю) и D_j = с_БА _j - c_j.

Если в индексной строке m элементов равны нулю, а остальные неотрицательны, то оптимальный план для max z имеет вид:

Если в индексной строке m элементов равны нулю, а остальные неположительные то это оптимальный план для min z.

Пример: Решить ЗЛП

Min z = 2x₁-x₂+3x₃-2x₄+1,5x₅

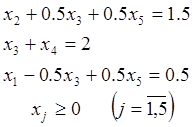
БП	cБ	А0	х1	х2	х3	х4	х5
			2	-1	3	-2	1,5
x2 x4 x1	-1 -2 2	1,5 2 0,5	0 0 1	1 0 0	0,5 1 -0,5	0 1 0	0,5 0 0,5
∆j		-4,5	0	0	-6,5	0	-1

Все оценки индексной строки неположительны. Значит, план (см. столбец А₀).

является оптимальным.

Целевая функция достигает значения.

6.5. Переход к нехудшему опорному плану

Положим, что задача линейного программирования представлена в предпочтительном виде:

;

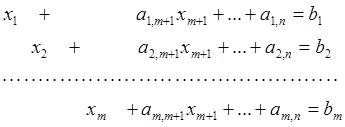                                          (6.6)

где b_i ³ 0; x_j ³ 0   (i = ; j = ).

Следовательно, начальный опорный план имеет следующий вид :

В разделе 6.3 целевая функция была выражена через свободные переменные с помощью формулы:

,                                                 (6.7)

где

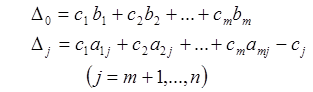
причем D _j - числа индексной строки симплекс-таблицы.