Линейное программирование. Задача линейного программирования (ЗЛП), страница 9

Первое ограниченное имеет предпочтительную переменную х₄ второе и третье – предпочтительных переменных не имеют. Для придания второму и третьему ограничениям предпочтительного вида введем искусственные переменные w₁ и w₂. Получим

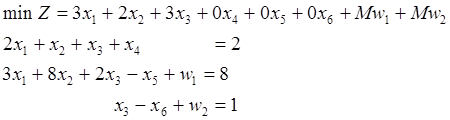
Введя искусственные переменные, индексную строку в симплексной таблице удобно разбить на две. Составим симплексную таблицу и выполним преобразования.

№ итерации	БП	сБ	А0	х1	х2	х3	х4	х5	х6	w1	w2	Симплексные отношения
				3	2	3	0	0	0	M	M
1	x4	О	2	2	1	1	1	0	0	0	0	2/1 = 2
	w1	М	8	3	8	2	0	-1	0	1	0	8/8 =1
	w2	М	1	0	0	1	0	0	-1	0	1	-
	Dj		0	-3	-2	-3	0	0	0	0	0
			9М	3М	8М	3М	0	-М	-М	0	0
2	x4	0	1	13/8	0	3/4	1	1/8	0	-1/8	0	1/(3/4)=4/3
	x2	2	1	3/8	1	1/4	0	-1/8	0	1/8	0	1/(1/4)=4
	w2	М	1	0	0	1	0	0	-1	0	1	1/1 = 1
	Dj		2	-9/4	0	-5/2	0	-1/4	0	1/4	0
			М	0	0	М	0	0	-М	-М	0
3	x4	0	1/4	13/8	0	0	1	1/8	3/4
	x2	2	3/4	3/8	1	0	0	-1/8	1/4
	х3	3	1	0	0	1	0	0	-1
	Dj		9/2	-9/4	0	0	0	-1/4	-5/2	-М	-М

После третьей итерации все числа в индексной строке не положительные, следовательно - минимум достигнут. Оптимальный план имеет вид x* = (0, ¾, 1, ¼, 0), причем z(x*) = 9/2

7.3. Решение ЗЛП на персональном компьютере

Программное обеспечение персональных компьютеров существенно упрощает решение задач линейного программирования. Рассмотрим решение ЗЛП с использованием системы MATHCAD.

Для решения задачи выполняют следующие действия в оболочке системы MATHCAD.

·  Определяют функцию, максимум или минимум которой надо найти.

·  Указывают приближенные значения переменных, значения которых надо определить.

·  Вводят слово Given, обозначающее начало блока решения задачи.

·  Ниже слова Given, используя булевы операторы,  вводят равенства и неравенства, служащие ограничениями.

·   Вводят функцию Minimize или Maximize с соответствующими аргументами.

Формат функций Minimize и Maximize:

Minimize(f, v1, v2, …) - функция возвращает значения v1, v2, … , удовлетворяющие ограничения, содержащиеся в блоке решения задачи, и дающие минимум функции f;

Maximize(f, v1, v2, …) - функция возвращает значения v1, v2, … , удовлетворяющие ограничения, содержащиеся в блоке решения задачи, и дающие максимум функции f.

Если условия задачи на минимум или максимум не содержат ограничений, то слово Given можно не вводить.

Рассмотрим пример решения средствами системы MATHCAD следующей ЗЛП с поиском минимума целевой функции.

Целевая функция -

Ограничения -

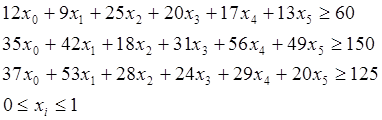
Оптимальный план, найденный симплексным методом -

(1;   0,623;   0,343   1;   0,048)

Решение этой задачи с помощью системы MATHCAD.

 -

Контрольные вопросы

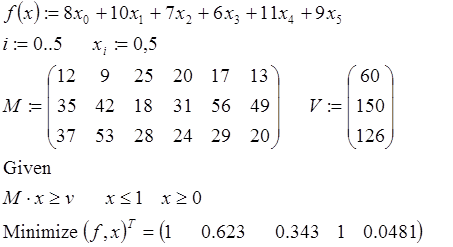32.  Как привести ЗЛП к канонической форме.

33.  Как привести ЗЛП к предпочтительному виду.