Пусть ищем max z.
И пусть не все числа индексной строки неотрицательны. Например, отрицателен
индекс с номером j (![]() < 0). Тогда значение
целевой функции z не максимально и его можно увеличить, увеличив xj. При этом xj перестанет
быть равным нулю. Но число равных нулю переменных xi должно остаться прежним и равным n-m.
Значит, вместо xj должна обратиться в ноль одна из базисных переменных,
иначе такой набор х не будет опорным планом. А хj станет базисной
переменной вместо xi. Выполним
такое преобразование.
< 0). Тогда значение
целевой функции z не максимально и его можно увеличить, увеличив xj. При этом xj перестанет
быть равным нулю. Но число равных нулю переменных xi должно остаться прежним и равным n-m.
Значит, вместо xj должна обратиться в ноль одна из базисных переменных,
иначе такой набор х не будет опорным планом. А хj станет базисной
переменной вместо xi. Выполним
такое преобразование.
Одно из уравнений (6.6) преобразуем так, чтобы у xiкоэффициент стал равен 1. Пусть это будет, например, i-ое уравнение (i-ая строка симплекс-таблицы). Это уравнение имеет вид:
xi + ai,m+1 xm+1 + … + ai,j xj +… + ainj xn = bi. (6.8)
Сделаем хi свободной переменной, а хj - базисной. Для этого надо, чтобы коэффициент при хj стал равен 1, для чего разделим все уравнение на аij. Для наглядности переменную хj поменяем ее местами с хi. Получаем уравнение
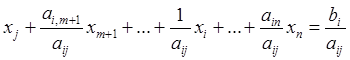 (6.9)
(6.9)
Строка симплекс-таблицы, в которой элементы преобразуются по формуле (6.9), называется ключевой строкой.
Установим, какую из строк симплекс-таблицы можно избрать в качестве ключевой.
Учитывая, что свободные переменные xm+1= xm+2 =…= xn = 0, имеем xj = bi ¤aij. Для того, чтобы выполнялось условие xj > 0, должно быть aij > 0. При выборе ключевой строки это требование надо учитывать.
Чтобы системе ограничений придать предпочтительный вид, в остальных уравнениях (и строках симплекс-таблицы), кроме i-ой, переменная xj должна исчезнуть. Рассмотрим одну из таких строк, например, m-ю:
![]() (6.10)
(6.10)
Исключим хj, для чего подставим на место хj в уравнение (6.10) вытекающее из (6.9) выражение:
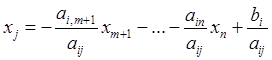 (6.11)
(6.11)
Получим
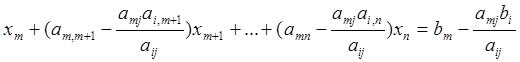 (6.12)
(6.12)
Теперь, чтобы при xm+1=
xm+2 =…= xn = 0
обеспечить положительное значение xm , надо, чтобы дробь 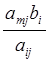 была
возможно меньше. Следовательно, в качестве i-ой строки
надо выбирать такую, в которой
была
возможно меньше. Следовательно, в качестве i-ой строки
надо выбирать такую, в которой ![]() минимальное.
минимальное.
В связи с заменой базисной переменной в целевой функции в результате подстановки (6.11) в (6.7) вместо хj возникает хi:
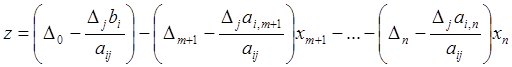 (6.13)
(6.13)
Поскольку
![]() - свободные переменные, которые в опорном
плане равны нулю, получаем
- свободные переменные, которые в опорном
плане равны нулю, получаем
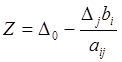 .
.
Если исходный опорный план оказался неоптимальным (см. раздел 6.3), необходимо перейти к другому, нехудшему плану, выполнив преобразования в симплекс-таблице.
Порядок перехода от исходного опорного плана к нехудшему.
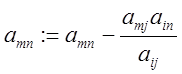 , где aij - ключевое число.
, где aij - ключевое число.
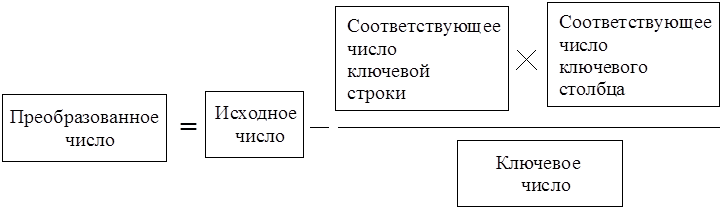
Расположение элементов формулы в симплекс-таблице показано в следующей схеме, изображающей фрагмент таблицы
|
Ключевая строка |
aij |
… |
ain |
|
… |
… |
||
|
Строка m |
amj |
… |
amn |
|
Ключевой столбец |
Столбец m |
Напишем еще мнемоническую формулу преобразования чисел симплекс-таблицы.
6.7. Особые случаи.
Альтернативный оптимум.
Если в индексной строке симплекс-таблицы, содержащей оптимальный план, имеется лишний ноль (в столбике свободной переменной), то ЗЛП имеет бесконечно много равноценных оптимальных планов.
Докажем это утверждение.
Пусть ∆k = 0, где k - номер свободной переменной xk. Введем xk в базис, то есть сделаем ее базисной переменной. Новое значение целевой функции найдем по формуле (6.13). Получим
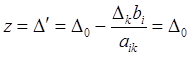 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.