Линейное программирование. Задача линейного программирования (ЗЛП), страница 8

Сформулируем математическую модель задачи:

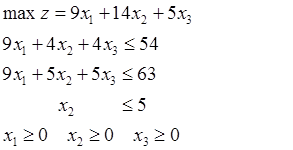
Для приведения ЗЛП в каноническую форму введем дополнительные неизвестные х₄, х₅, х₆, смысл которых – остатки сырья на складе после выполнения плана.

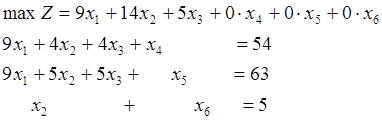
Задача имеет предпочтительный вид, что позволяет составить начальный опорный план  (0; 0; 0; х₄; х₅; х₆) = (0; 0; 0; 54; 63; 5). Этот план означает, что выпуска продукции нет, и все сырье остается на складе. Для поиска оптимального плана составим симплексную таблицу. Ключевые числа в таблице обведены утолщенной рамкой.

№ итерации	БП	сБ	А0	х1	х2	х3	х4	х5	х6	Симплексные отношения
				9	14	5	0	0	0
1	х4	0	54	9	4	4	1	0	0	54/4=13
	х5	0	63	9	5	5	0	1	0	63/5=12
	х6	0	5	0	1	0	0	0	1	5/1=5
	Dj		0	-9	-14	-5	0	0	0
2	х4	0	34	9	0	4	1	0	-4	34/9
	х5	0	38	9	0	5	0	1	-5	38/9
	х2	14	5	0	1	0	0	0	1	-
	Dj		70	-9	0	-5	0	0	14
3	х1	9	34/9	1	0	4/9	1/9	0	-4/9	34/4=8.5
	х5	0	4	0	0	1	-1	1	-1	4/1=4
	х2	14	5	0	1	0	0	0	1	-
	Dj		104	0	0	-1	1	0	10
4	х1	9	2	1	0	0	5/9	-4/9	0
	х3	5	4	0	0	1	-1	1	-1
	х2	14	5	0	1	0	0	0	1
	Dj		108	0	0	0	0	1	9

Видим, что после выполнения четвертой итерации отрицательных чисел в индексной строке нет. Оптимальный план составлен он имеет вид: х₁ = 2; х₂ = 5; х₃ = 4. Прибыль составляет D₀ = 108.

Все сырье истрачено:

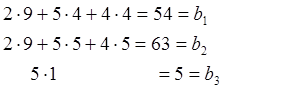
Альтернативный оптимум.

В индексной строке найденного решения ЗЛП вместо трех нулей – четыре. Следовательно, как показано в разделе 6.7, существуют и иные планы, обеспечивающие такой же оптимум. Сделаем в последней симплекс-таблице новой базисной переменной х₄ и выполним симплексные преобразования. Получим  следующую таблицу:

№ итерации	БП	сБ	А0	х1	х2	х3	х4	х5	х6
				9	14	5	0	0	0
5	х4	0	18/5	9/5	0	0	1	- 4/5	0
	х3	5	38/5	9/5	0	1	0	1/5	-1
	х2	14	5	0	1	0	0	0	1
	Dj		108	0	0	0	0	1	0

Получили новый оптимальный план:

По новому плану продукт х₁ не выпускается. Прибыль та же - 108. Сэкономлено х₄=18/5=3,6 единицы сырья b₁. Сырье b ₂ и b ₃ использовано полностью.

Согласно доказанному в разделе 6.7, любой план следующего вида:

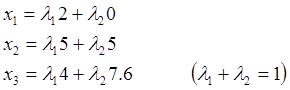
даст ту же прибыль.

7.2. Пример решения ЗЛП с искусственными переменными

Рассмотрим решение следующей ЗЛП на поиск минимума.

      - целевая функция

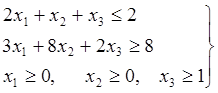  - ограничения

Приведем задачу к канонической форме, введя дополнительные переменные х₄, х₅, х₆.

x_j ³ 0         (j = )