8. НЕЛИНЕЙНЫЕ ОПТИМИЗАЦИОННЫЕ МОДЕЛИ
8.1. Общие сведения.
Построение оптимизационных моделей в тех случаях, когда целевая функция не является линейной, связано с решением задачи на поиск экстремума такой функции.
При этом возможны задачи, в которых ограничений на область значений переменных нет, и задачи, в которых область значений переменных ограничена.
Задачи без ограничений.
Решение такой задачи читателю знакомо из курса дифференциального исчисления, поэтому ограничимся кратким напоминанием.
Пусть max(min) z = f(x1, x2, … , xn) – целевая функция.
В точке экстремума функции z её первые производные, если они существуют, равны нулю. Найдем производные z по всем переменным и приравняем их нулю. Получим систему n уравнений с неизвестными x1, x2, … , xn
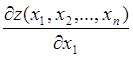 =0,
=0, 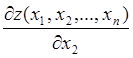 =0, … ,
=0, … , 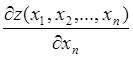 =0.
(8.1)
=0.
(8.1)
В случае выпуклой или вогнутой функции (см. ниже) решение этой системы уравнений сразу укажет точку x1, x2, … , xn экстремума функции. В более сложных случаях необходимо выполнить исследование на отсутствие в найденной точке минимакса функции z, то есть такого положения, что относительно одних xi функция имеет максимум, а относительно других – минимум.
Задачи с ограничениями.
Если область изменения переменных ограничена, то задача поиска экстремума их нелинейной функции носит название задачи нелинейного программирования.
Запишем задачу математического программирования в общем виде
max (min) z = f(![]() );
(8.2)
);
(8.2)
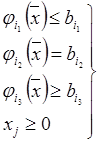 (8.3)
(8.3)
i1 = 1, 2, … , m1; i2 = m1 +1, m1+2, … , m2; i3 = m2 +1, m2+2, … , m;
j = 1, 2, … , n;
![]() = (x1,
x2, … , xn)
= (x1,
x2, … , xn)
Если целевая функция (8.2) или ограничения (8.3) нелинейны, то задача называется задачей нелинейного программирования.
Ввиду многообразия и сложности задач нелинейного программирования общего метода их решения не существует. Наиболее разработаны способы решения задач, относящихся к выпуклому программированию. Это такие задачи, где f(x) и ji(x) - выпуклые или вогнутые.
Функцию f(x) называют выпуклой,
если для любых точек ![]() и
и ![]() справедливо
неравенство
справедливо
неравенство
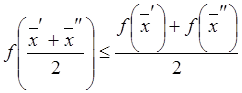 .
.
Функцию f(x) называют вогнутой,
если для любых точек ![]() и
и ![]() справедливо
неравенство
справедливо
неравенство
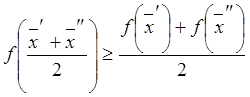 .
.
Иначе говоря, выпуклая функция - такая, у которой все точки отрезка, соединяющего две ее точки, лежат выше точек функции. У вогнутой функции все точки такого отрезка лежат ниже точек функции.
Двухмерный случай иллюстрируется рисунком, где в варианте а) показана выпуклая, а в варианте б) – вогнутая функция.
|
|
|
Особенностью выпуклой и вогнутой функций является наличие единственного экстремума. Другого вида функции могут иметь несколько локальных экстремумов, из которых один – глобальный.
В качестве основной в теории выпуклого программирования
рассматривают задачу минимизации выпуклой функции n переменных
z = f(![]() ) при ограничениях
) при ограничениях ![]() (i = 1, 2, … ,m),
(i = 1, 2, … ,m), ![]() ,где функции
,где функции ![]() предполагаются выпуклыми.
предполагаются выпуклыми.
Если f(![]() ) и
) и ![]() являются
вогнутыми функциями, то имеем задачу максимизации f(
являются
вогнутыми функциями, то имеем задачу максимизации f(![]() ) при ограничениях
) при ограничениях ![]() (i = 1, 2, … ,m),
(i = 1, 2, … ,m), ![]() .
.
8.2. Коррелатное уравнивание результатов геодезических измерений – задача выпуклого программирования
Целью уравнивания измерений является минимизация целевой функции
min z = p1v12 + p2v22 + … + pnvn2 где pi – веса и vi – поправки к результатам измерений (i = 1, 2, … , n). Поправки должны соответствовать ограничениям – условным уравнениям:
a11v1 + a12v2 + … + a1nvn + w1 = 0,
a21v1 + a22v2 + … + a2nvn + w2 = 0,
…………………………………...
am1v1 + am2v2 + … + amnvn + wm = 0.
Имеем выпуклую целевую функцию с линейными ограничениями.
Перепишем систему условных уравнений в матричной форме
AV + W = 0, (8.4)
где А – матрица коэффициентов, V – вектор поправок и W – вектор свободных членов.
Составим функцию Лагранжа, введя вспомогательные множители – коррелаты:
L = p1v12 + p2v22 + … + pnvn2 + 2 l1(w1 - a11v1 - a12v2 - … - a1nvn) +
+ 2 l2(w2 - a21v1 - a22v2 - … - a2nvn) +
……………………………………….
+ 2 lm(w m - a m 1v1 - a m 2v2 - … - a m nvn).
Поскольку при выполнении условий, сформулированных условными уравнениями, выражения в скобках равны нулю, экстремум функции Лагранжа совпадает с экстремумом целевой функции z. Для отыскания экстремума приравняем производные функции Лагранжа нулю:
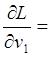 2 (p1v1
- l1a11 - l2a21- … - lmam1) = 0
2 (p1v1
- l1a11 - l2a21- … - lmam1) = 0
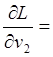 2 (p2v2
- l1a12 - l2a22- … - lmam2) = 0
2 (p2v2
- l1a12 - l2a22- … - lmam2) = 0
……………………………………………
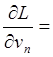 2 (pnvn
- l1a1n - l2a2n- … - lmamn) = 0
2 (pnvn
- l1a1n - l2a2n- … - lmamn) = 0
Полученную систему уравнений для сокращения последующих записей также перепишем в матричном виде:
PV - AТL = 0. (8.5)
Из (8.5) находим
V = P-1AТL. (8.6)
и подставим полученное выражение для вектора поправок в условное уравнение (8.4). Получаем систему нормальных уравнений
A P-1AТL + W = 0. (8.7)
Получили известные формулы коррелатного метода уравнивания.
Поправки к результатам измерений, минимизирующие целевую функцию, находим в следующем порядке. Решением нормальных уравнений (8.7) определяем вектор коррелат L. Подставляя коррелаты в (8.6), вычисляем вектор поправок к результатам измерений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.