Нелинейные оптимизационные модели, страница 8

Смещение рельса в точке i при его выправке равно:

Для левого рельса  v_i = y_i – l_lefti = a_i  y1+ b_i yn - l_lefti.

Для правого рельса v_i = y_i + S0 – (S_i+ l_righti) = a_i  y1+ b_i yn – l¢_righti, где l¢_righti = (S_i+ l_righti - S0).

Записанные в общем виде уравнения поправок (рихтовок) имеют вид

v_i = y_i – l_i = a_i × y1 + b_i ×  yn – l_i.

Поэтому целевая функция [vv] имеет вид

[vv] = [ll] - 2[al] y1 - 2[bl] yn + [aa] y1² + [bb] yn² + 2[ab] y1 yn .

Порядок вычислений

1. Вычисление междустворных расстояний в точках х₂ .. х₆.

S_i = a_i S₁ + b_i S_n , где 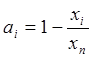   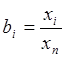 ;          (i = 2, ... ,n –1).    

2. Составление вектора L четырнадцати (то есть 2n) свободных членов уравнений поправок  для целевой функции

L_i = l_lefti ;     L_n+i = S_i+ l_righti - S0;    (i = 2, ... ,n –1).    

3. Приведение измеренных ограничений правого рельса к системе координат левого створа

tl¢_righti = S_i + tl_righti - S0

tr¢_righti = S_i + tr_righti - S0

4. Вычисление шести коэффициентов целевой функции: [ll], [al], [bl], [aa], [bb], [ab]. Здесь l – элементы вектора свободных членов L. Вычисление сумм с коэффициентами a и b упрощается, если предварительно составлены векторы A и B. Составляющими этих векторов являются дважды повторенный список коэффициентов a и b.

5. Организация решения задачи математического программирования, для чего необходимо:

·  Сформулировать целевую функцию

[vv] : = [ll] + 2[al] y1+ 2[bl] yn + [aa] y1² + [bb] yn² + 2[ab] y1 yn .

·  Написать блок ограничений, состоящий из слова “Given” и списка 28 ограничений. Например,

Given

a₁ y1 + b₁ yn – tlleft₁ ³ Q  

…………………………

…………………………

………………………….

- a₇ y1- b₇ yn+ tr¢right₇ ³ Q  

·  Написать команду минимизации целевой функции и выдачи коэффициентов y1, yn оптимальной прямой

Y : = Minimize (z, y1, yn)       Y =  

6. Составление двух таблиц данных (номера точек, ординаты у, смещения v) для рихтовки рельсов. Например, первая таблица – для левого рельса, может быть составлена так:

NN_i = i        yi = a_i× y1 + b_i× yn       vi = yi - l_lefti

Контрольные вопросы

22.  Что является признаком нахождения точки на границе допустимой области?

23.  Какими формулами определяется направление движения по границе допустимой области в сторону максимума?

24.  Какими формулами определяется направление движения по границе допустимой области в сторону минимума?

25.  По какой формуле определяется признак достижения экстремума на границе допустимой области?

26.  Какими формулами определяется длина шага l при движении по границе допустимой области?

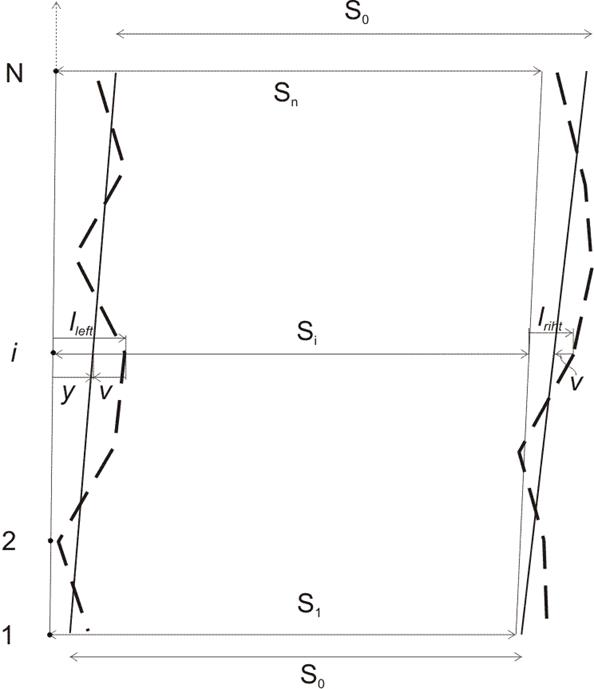
Рис. 1.  Расположение створов и подкрановых рельсов: тонкие линии – створы (левый и правый); утолщенные линии – выправленное положение рельсов; штриховые линии – первоначальное положение рельсов; S₁ и S_n – измеренные междустворные расстояния; S₀ – проектное расстояние между рельсами; l_left и l_right – измеренные расстояния от створов до рельсов, левого и правого; y – расчетное расстояние от левого створа до выправленного рельса; v – рихтовки.

Рис. 2  Измеряемые элементы и ограничения: l_left и l_right – измеренные расстояния от левого и правого створа до соответствующих рельсов; tl_left и tr_left – расстояния до левого и правого ограничивающих препятствий на левом створе; tl_right и tr_right – расстояния до левого и правого ограничивающих препятствий на правом створе; Q – габаритное ограничение.

ЛИТЕРАТУРА

1.  Мышкис А.Д. Элементы теории математических моделей. – М.: Физматлит, 1994.

2.  Кузнецов А.В. и др. Высшая математика. Математическое программирование: Учебник. – Мн.: Высш. шк., 1994.

3.  Сборник задач и упражнекний по высшей математике. Математическое программирование: Учебное пособие. – Мн.: Высш. шк., 1995.

4.  Брыкин П.Ф., Кимельман С.А. Математическое программирование в планировании геодезических и топографических работ.  – М.: Недра, 1972.

5.  Херхагер М., Парголль Х., Mathcad 2000: полное руководство: Пер. с нем. – К.: Издательская группа BHV, 2000.