Нелинейные оптимизационные модели, страница 3

-  по формулам, полученным дифференцированием целевой функции z = f ();

-  численным методом.

Вычисление приближенных значений производных численным методом покажем на примере производной по переменной x_i.  Переменную x_i увеличивают и уменьшают на малую величину e, оставляя остальные переменные без изменений. При обоих измененных значениях переменной x_i вычисляют значения целевой функции и образуют их разность, которую делят на 2e. Напишем соответствующую формулу

.

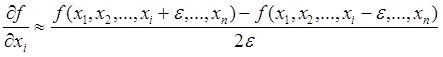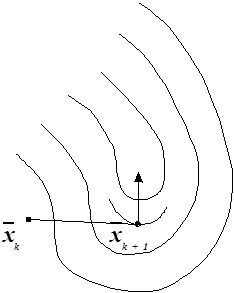
Величина шага зависит от выбора параметра l. Слишком малый шаг ведет к замедлению процесса приближений к экстремуму. Большой шаг ведет к «проскакиванию» мимо точек изменения направления градиента и самой точки экстремума . Иногда величину шага принимают пропорциональной модулю градиента.

Признаком выхода в точку  служит равенство нулю градиента Ñf ().

9.3. Метод наискорейшего подъема (спуска)

Рассмотрим случай подъема, то есть поиск максимума  функции f ().

Из каждой точки шаг по направлению градиента делают до такой точки , в которой на этом направлении достигается максимум функции f (). В точке   прежнее направление градиента является касательным к линии уровня функции f (). Поэтому градиент в точке    перпендикулярен предыдущему, то есть градиенту в точке . Следовательно, скалярное произведение рассматриваемых градиентов равно нулю

Это равенство позволяет определить длину шага (точнее – множитель l).

Следующий шаг делают в направлении нового градиента.

В случае поиска минимума  функции f () движение происходит в направлении антиградиента и говорят о методе наискорейшего спуска.

Пример:

Определить максимум функции  f = 4x +8y-2x² – 2y² .

Градиент функции равен 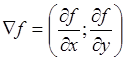= (- 4x +4; - 4y + 8).

Начнем поиск из точки = (5; 10), то есть из точки х₀ = 5;  у₀ = 10.

В этой точке градиент равен:

Первый шаг - в точку                 ;

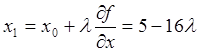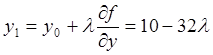
Градиент в точке  Ñf₁ = Ñf(5 - 16l; 10 - 32l) = (-16 + 64l; -32 + 128l)

Равенство скалярного произведения градиентов нулю в нашем примере дает

-16 (-16 + 64l) - 32(-32 + 128l) = 0, откуда получаем l = ¼ .

Следовательно, в точке 1 координаты и градиент равны: x₁ = 5 - 16×¼ = 1; y₁ = 10 - 32×¼ = 2;;; = (0; 0).

Поскольку в точке 1 градиент равен нулю, максимум функции f найден. Он находится в точке с координатами х₁ = 1; у₁ = 2 и равен  

9.4. Уравнивание геодезической сети градиентным методом

Для определения вектора координат пунктов

выполнены измерения. Получен вектор результатов измерений:

       (n > k)

Зададимся приближенными координатами  и вычислим по ним приближенные значения измеренных величин - 

Начнем поиск из приближенной точки и на каждом шаге поиска будем уточнять вектор координат Х', добиваясь уменьшения вектора разностей между компонентами вычисленного вектора U¢ и измеренного вектора U:

                                                          (9.1)

Замечаем, что вектор V, является функцией от вектора приближенных координат, так как вычисляется по вектору U'. Перепишем равенство (9.1) подробнее:

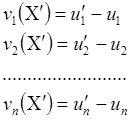
Для реализации принципа наименьших квадратов, целевая функция должна иметь вид . В другой – матричной записи:

min z(X¢) = V(Х¢)^Т × P×V(Х¢),                                          (9.2)

где Р – весовая матрица.

Видим, что и целевая функция является функцией от приближенных координат.

Для перехода от приближенной точки Х' к лучшей точке Х'' воспользуемся градиентным методом. Градиент целевой функции имеет вид

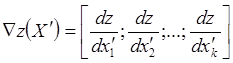                                  (9.3)

Значения составляющих градиента – частных производных целевой функции найдем численным методом. В векторе  изменим первую координату на малую величину ε и найдем два близких к Х' вектора:  и . Приближенное значение первой частной производной будет вычислено по формуле

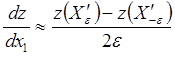                                                      (9.4)