Нелинейные оптимизационные модели, страница 6

,

½½=1.

Ограничение ½½=1 введено для того, чтобы как-то зафиксировать длину вектора , которая без этого неопределенна.

Длину шага  определим так же, как и в пункте 1, то есть до максимума , но не выходя за границы.

3.  Конец поиска.

Признаком максимума целевой функции в точке k является выполнение условия:

Примечание: Длина вектора  безразлична. Обычно принимают .

Пример.

Найти max функции  с учетом ограничений:

;

;                                                                                                 (9.16)

x ³ 0; y ³ 0.

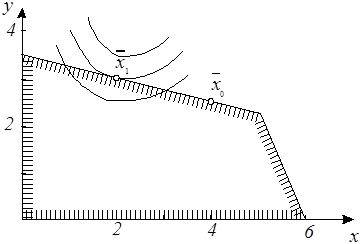
Решение.

1.  За начальную примем точку х₀ на граничной линии х + 4у = 14.

Конкретно положим х = 4. Тогда у = 2,5. Итак,  = (4; 2,5). Значения целевой функции и ее градиента в начальной точке :

= 4 + 2×2,5 - 0,2×16 - 0,2×2,5² = 4,55;

 = (1 - 0,4х; 2 - 0,4у);

 = (-0,6; 1).

По направлению градиента из точки  двигаться нельзя – не позволяет граница допустимой области. Надо двигаться по границе.

2.  Определим варианты направления из точки  вдоль ограничивающей линии. Обозначим направляющий вектор = (r_x; r_y), где r_x – проекция вектора  на ось х и r_y – проекция на ось у.

Двигаться по границе – значит, изменяя х и у, не нарушить равенство х + 4у = 14. Для этого необходимо, чтобы (см. 9.14)

r_x + 4r_y = 0.

Например, годятся варианты: 1) r_x = 4, r_y = -1;   2) r_x = -4, r_y = 1.

Нормируем длину вектора  так, чтобы ½½=1, для чего разделим его составляющие r_x и r_y  на   = = 4,1231.

Получаем два варианта направления: 1) r_x = 0,9701,  r_y = -0,2425;   2) r_x = -0,9701,  r_y = 0,2425.

3.  Выбор направления.

В соответствии с (9.15) из двух вариантов направления выбрать надо то, которое дает максимум скалярному произведению = - 0,6×r_x + 1× r_y .

Подсчитаем скалярные произведения конкурирующих вариантов:

1) -0,6× 0,9701 + 1×(-0,2425) = -0,8246 < 0;

2) -0,6×(-0,9701) + 1× 0,2425 = 0,8246 > 0.

Очевидно, из двух вариантов следует выбрать второй. Итак,

= (r_x; r_y) = (-0,9701; 0,2425).

4.  Координаты x₁, y₁ следующей точки , записанные в общем виде:

x₁ = x₀ + l×r_x = 4 - 0,9701 l,

y₁ = y₀ + l×r_y = 2,5 + 0,2425 l.

5.  Определение допустимого диапазона значений l.

Точки  и  лежат на ограничивающей линии х + 4у = 14, так что первое из ограничений (9.16) удовлетворено. Рассмотрим влияние на коэффициент  остальных трех ограничений:

Ограничение  дает 7(4 – 0,9701l) + 3(2,5 + 0,2425l) £ 42, то есть  l ≥ - 1,0722.

Ограничение x ≥ 0 дает 4 – 0,9701l ≥ 0, то есть  l  £ 4,1237

Ограничение y ≥ 0 дает 2,5 + 0,2425l ≥ 0, то есть  l ≥ - 10,3 .

Отрицательные значения l нас не интересуют, они означали бы движение в направлении, противоположном выбранному в пункте 3.

Поэтому значения l должны лежать в диапазоне [0;  4,1237].

6.  Определение значения l, при котором на прямой  достигается максимум.

Признак максимума - равенство нулю скалярного произведения  .

= (1 - 0,4х₁; 2 - 0,4у₁) =  (-0,6 + 0,388l; 1 - 0,097l);

= (-0,9701; 0,2425);

 = 0,582 - 0,376l + 0,2425 - 0,0235l = 0,8245 - 0,3999l = 0.

Откуда l = 2,0618.

Следовательно, на прямой х₀х₁ максимум функции  достигается при значении l = 2,0618.

7.  Выбор значения .

В пункте 5 установлено, что параметр l должен находиться в диапазоне  [0;  4,1237]. В пункте 6 установлено, что максимум   наступает при значении l = 2,0618, которое вписывается  в допустимый диапазон [0; 4,1237]. Поэтому принимаем окончательно l = 2,0618.

8.  Вычисление координат точки  

 = 4 - 2,0618×0,9701 = 2;

= 2,5 - 2,0618×0,2425 = 3.

9.  Проверка точки  на экстремум.

= (1 - 0,4х₁; 2 - 0,4у₁) =  (0,2;  0,8);

=  = (-0,9701; 0,2425);

 = - 0,2×0,9701 + 0,8×0,2425 = 0.

Скалярное произведение равно нулю. Значит, максимум функции f найден и располагается в точке с координатами х₁ = 2; у₁ = 3. При этом значение максимума равно

9.6. Решение задач выпуклого программирования на персональном компьютере с помощью систем MATHCAD.