1. Что такое - задача выпуклого программирования с вогнутой целевой функцией и линейными ограничениями?
2. Что такое - задача выпуклого программирования с выпуклой целевой функцией и линейными ограничениями?
3. Какие существуют и как выглядят ограничения в задаче выпуклого программирования?
4. Каковы целевая функция и ограничения при коррелатном методе уравнивания геодезических измерений?
9. Градиентные методы РЕШЕНИЯ ОПТМИЗАЦИОННЫХ ЗАДАЧ
9.1. Основные сведения
Идея градиентного метода поиска экстремума целевой функции состоит в следующем. Назначив в допустимой области произвольную точку, вычисляют градиент целевой функции, который указывает направление её возрастания. Сделав шаг в направлении градиента, получают новую точку и вычисляют новое направление. Постепенно приходят в точку максимума.
Для поиска минимума поступают аналогично, двигаясь по направлению антиградиента.
Отметим, что градиентный метод способен найти только ближайший к начальной точке локальный экстремум. В случае выпуклой функции, он же является и глобальным.
Благодаря простоте алгоритма градиентный метод применяется для решения широкого круга оптимизационных задач.
Градиентный метод может быть использован и для уравнивания геодезических сетей, позволяя создание более простых алгоритмов и обеспечивая возможность решения задачи уравнивания с целевой функцией, отличной от min[pv2]. Такая возможность может оказаться очень полезной, поскольку возможны случаи, когда целесообразно вместо суммы квадратов поправок минимизировать сумму их модулей или, например, сумму их четвертых степеней. Изучение конечных методов решения таких задач потребовало бы серьезных усилий, тогда как применение градиентного метода значительно проще.
Приведем необходимые сведения о градиентах на примере
двухмерного пространства переменных. Пусть ![]() -
целевая функция и
-
целевая функция и 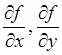 - ее частные производные,
представляющие собой скорости изменения функции z в
направлении осей х и y. Зная скорости изменения функции z в направлении осей х
и y, можем указать скорость изменения той же функции в
любом направлении a, где α – угол с
осью х. Она равна сумме проекций составляющих скоростей на это
направление:
- ее частные производные,
представляющие собой скорости изменения функции z в
направлении осей х и y. Зная скорости изменения функции z в направлении осей х
и y, можем указать скорость изменения той же функции в
любом направлении a, где α – угол с
осью х. Она равна сумме проекций составляющих скоростей на это
направление:
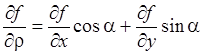 .
.
Градиентом функции ![]() в
точке М называется вектор, имеющий координатами частные производные
функции z, вычисленные
в этой точке.
в
точке М называется вектор, имеющий координатами частные производные
функции z, вычисленные
в этой точке.
Будем применять следующие обозначения градиента: ![]() ; grad f(x,
y);
; grad f(x,
y); ![]() .
.
Следовательно, согласно определению градиента
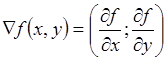 .
.
Очевидно, модуль градиента, ½![]() ½равен
½равен
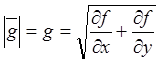 .
.
Модуль градиента ½![]() ½равен
наибольшей скорости возрастания функции. Направление градиента – направление
наискорейшего возрастания функции. В каждой точке х, у градиент
функции f(x, y) направлен по нормали к линии уровня поверхности
½равен
наибольшей скорости возрастания функции. Направление градиента – направление
наискорейшего возрастания функции. В каждой точке х, у градиент
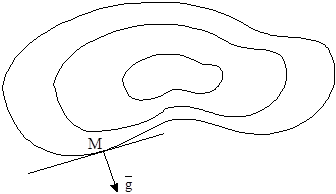
функции f(x, y) направлен по нормали к линии уровня поверхности ![]() , проходящей через эту точку. На рисунке
показаны линии уровня функции f(x, y), касательная к линии
уровня в точке M и перпендикулярный к ней
градиент
, проходящей через эту точку. На рисунке
показаны линии уровня функции f(x, y), касательная к линии
уровня в точке M и перпендикулярный к ней
градиент ![]() .
.
В многомерном случае градиент имеет вид 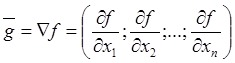 , а модуль градиента равен
, а модуль градиента равен 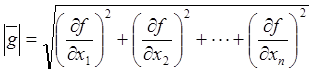 .
.
9.2. Решение градиентным методом оптимизационной задачи без ограничений
Рассмотрим задачу поиска максимума дифференцируемой
функции z = f (![]() ), где
), где ![]() – вектор координат точки. В n-мерном
пространстве
– вектор координат точки. В n-мерном
пространстве ![]() = (x1, x2, … , xn).
= (x1, x2, … , xn).
Пусть функция f (![]() )
достигает максимума в точке
)
достигает максимума в точке ![]() . Начнем поиск в
произвольной точке
. Начнем поиск в
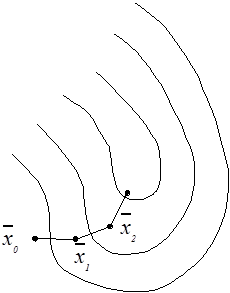
произвольной точке ![]() (см. рис.). Вычислим направление
градиента Ñf (
(см. рис.). Вычислим направление
градиента Ñf (![]() ). В этом направлении сделаем шаг и попадем в точку
). В этом направлении сделаем шаг и попадем в точку ![]() . Из новой точки в направлении нового
градиента - еще шаг. При этом c каждым шагом
значение функции будет возрастать до тех пор, пока не выйдем в точку ее
максимума
. Из новой точки в направлении нового
градиента - еще шаг. При этом c каждым шагом
значение функции будет возрастать до тех пор, пока не выйдем в точку ее
максимума ![]() .
.
Шаг из точки хk в точку хk+1 в двухмерном случае описывается формулами
xk+1 = xk+1 + lk 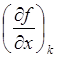 ; yk+1 = yk+1
+ l k
; yk+1 = yk+1
+ l k 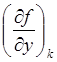 ;
;
Если имеем многомерный случай, то формула для того же шага будет иметь вид
![]() .
.
Вычисление частных производных – компонентов градиента возможно двумя методами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.