Нелинейные оптимизационные модели, страница 7

Порядок действий при решении задачи выпуклого программирования с помощью системы MATHCAD мало отличается от решения задач линейного программирования.

Как и при решении ЗЛП необходимо выполнить следующие действия.

·  Определить (то есть записать в символах системы MATHCAD) функцию, максимум или минимум которой надо найти.

·  Указать приближенные значения переменных, значения которых надо определить.

·  Написать слово Given, обозначающее начало блока решения задачи.

·  Ниже слова Given, используя булевы операторы,  записать равенства и неравенства, служащие ограничениями.

·   Ввести функцию Minimize или Maximize с соответствующими аргументами.

Формат функций Minimize и Maximize такой же, как и в случае ЗЛП:

Minimize(f, v1, v2, …) - функция возвращает значения v1, v2, … , удовлетворяющие ограничения, содержащиеся в блоке решения задачи, и дающие минимум функции f;

Maximize(f, v1, v2, …) - функция возвращает значения v1, v2, … , удовлетворяющие ограничения, содержащиеся в блоке решения задачи, и дающие максимум функции f.

Если условия задачи на минимум или максимум не содержат ограничений, то слово Given можно не вводить.

Проиллюстрируем применение системы MATHKAD для решения задачи выпуклого программирования на том же примере, решение которого выполнено в разделе 9.7.

x := 4      y := 2.5

Given

x ³ 0        y ³ 0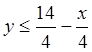              

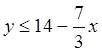
P := Maximize(f,x,y)

P =         f(P₀,P₁) = 5.4

9.7. Расчет рихтовки подкрановых путей методом выпуклого программирования

Рассмотрим решение на персональном компьютере с использованием системы MATHCAD следующей задачи. По результатам съемки подкрановых путей необходимо рассчитать смещения рельсов для их выпрямления.

Сумма квадратов смещений должна быть минимальной с учетом имеющихся ограничений на величину этих смещений.

Исходные данные

Вдоль рельсов подкранового пути закреплены два створа (ниже см. рис. 1). Измеренное расстояние между створами в их начале равно S₁=17002 мм, в конце – S_n=17022, где n=7. Расстояние между рельсами после рихтовки должно быть равно S₀=17000 мм.

Напротив колонн, поддерживающих подрельсовые балки, в семи точках, через 12 м измерены отклонения каждого рельса от своего створа (отклонение левого рельса l_left и правого - l_right), а также расстояния до препятствий, ограничивающих смещения рельсов при рихтовке (см. рис. 2). Знак плюс присвоен отклонениям вправо, минус – отклонениям влево.

Обозначим расстояния вдоль линии створа от его начала до точек с измерениями через х, а расстояния от створов до препятствий, ограничивающих смещения рельсов влево и вправо для левого рельса соответственно tl_left и tr_left и для правого рельса – tl_right и tr_right. Измеренные отклонения вправо считаем положительными, влево – отрицательными.

Следующее дополнительное ограничение принято общим для всех точек с измерениями. Ось рельса не может быть приближена к препятствию ближе, чем на Q = 20 мм.

Математическая модель задачи

Уравнение выправленного левого рельса будем искать в виде

y_i = a_i × y1 + b_i ×  yn, где a_i и b_i – заданные расстояния вдоль створа, выраженные в долях длины створа и считаемые: a_i – от конца створа и b_i – от начала створа;y1, yn – искомые расстояния до выправленного рельса от левого створа соответственно в первой и последней точках.

Соответствующие ординаты выправленного правого рельса будут равны  y_i + S₀.

При введенных обозначениях ограничения будут иметь следующий вид (см. рис. 2).

Для левого рельса:

- ограничение слева            y_i – tl_lefti ³ Q     или   a_i y1 + b_i yn – tl_lefti ³ Q  

- ограничение справа      - y_i + tr_lefti ³ Q     или  - a_i y1 - b_i yn + tr_lefti ³ Q

Для правого рельса:

- ограничение слева   (y_i+S0) – (S_i+ tl_righti) ³ Q, или  a_i  y1+ b_i yn - (Si + tl_righti - S0)³ Q  

- ограничение справа -(y_i+S0) +(S_i+ tr_righti) ³ Q, или - a_i  y1- b_i yn+ (Si + tr_righti - S0)³ Q  

Здесь S_i – расстояние между створами в точке i.