![]() выбираем так, чтобы она была
равна 1 в объеме и 0 везде вне объема. Вариант взвешенных невязок называют МКО.
выбираем так, чтобы она была
равна 1 в объеме и 0 везде вне объема. Вариант взвешенных невязок называют МКО.
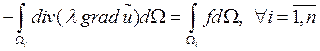
По формуле Остроградского-Гаусса:
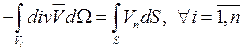
![]() -граница.
-граница. ![]() –
векторное поле.
–
векторное поле. ![]() – компонента поля.
– компонента поля.
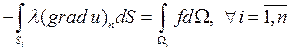
Стационарный процесс в области ![]() , тогда интеграл представляет собой
суммарный поток тепла через границу КО
, тогда интеграл представляет собой
суммарный поток тепла через границу КО 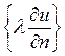 .
.
Правая часть![]() интеграл от плотности
тепловых источников, находящихся в КО.
интеграл от плотности
тепловых источников, находящихся в КО.
Необходимо учитывать, что на границе области – неполный КО.
Итерационный метод:
Последний элемент в матрице Хессенберга – норма невязки!
Пусть дана система: ![]() (1) где
(1) где ![]() - действительная невырожденная
матрица.
- действительная невырожденная
матрица.
Цель: решить СЛАУ, воспользовавшись проекционными методами.
Найти некоторое приближенное решение из подпространства ![]() , если
, если ![]() -искомое
подпространство и
-искомое
подпространство и ![]() -его размерность, то необходимо
определить
-его размерность, то необходимо
определить ![]() условий, из которых найти решение в
подпространстве
условий, из которых найти решение в
подпространстве ![]() размерности
размерности ![]() , т.е придумать и реализовать
, т.е придумать и реализовать ![]() условий.
условий.
Пусть формирование этих условий – введение ![]() независимых условий ортогональности,
например,
независимых условий ортогональности,
например, ![]() - вектор невязки, значит он должен быть
ортогонален некоторым
- вектор невязки, значит он должен быть
ортогонален некоторым ![]() линейно независимым векторам. Эти
линейно независимым векторам. Эти
![]() векторов формируют подпространство
векторов формируют подпространство![]() – подпространство ограничений. Это условие
называется условием Петрова-Галеркина.
– подпространство ограничений. Это условие
называется условием Петрова-Галеркина.
Методы
1.
Ортогональные:![]()
2.
Не ортогональные:![]() позволяет
сконструировать много методов
позволяет
сконструировать много методов
Проекционная техника на подпространство ![]() и ортогонально
и ортогонально ![]() – есть
процесс, позволяющий найти приближенное решение
– есть
процесс, позволяющий найти приближенное решение ![]() с
помощью введения условий:
с
помощью введения условий: ![]() . F новый вектор невязки
. F новый вектор невязки ![]() .
.
Тогда сформулируем задачу:
Найти ![]() при условии
при условии ![]() .
.
![]() порождает квадратичный выпуклый
функционал.
порождает квадратичный выпуклый
функционал.
Рассматриваются два типа задач:
![]() -
скорость,
-
скорость, ![]() - давление. В смешанной постановке
- давление. В смешанной постановке ![]() и
и ![]() ищутся
в разных функциональных пространствах.
ищутся
в разных функциональных пространствах.
Ограничение: ![]()
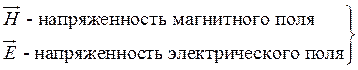 характеристики
поля
характеристики
поля
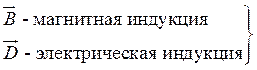 характеристики
потока
характеристики
потока
Ограничения: ![]() ,
, ![]() .
.
В разрывной области характеристики магнитного поля требуют непрерывности тангенциальных компонент, а характеристики электрического поля - непрерывности нормальных компонент.
Для магнитного поля хотя и требуется непрерывность тангенциальных компонент, но нужно сохранить скачок нормальных компонент на границе разрыва. Уравнения Максвелла можно решать как уравнения первого порядка, а можно как второго (эллиптическая, параболическая, гиперболическая).
В векторном МКЭ непрерывность нужной компоненты поля обеспечивает базис.
 Существуют два типа элементов:
Существуют два типа элементов:
Ориентация в пространстве:
Направление от меньшего к большему.
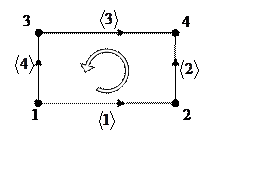

Связываем направление ребер с направлением осей ![]() .
.
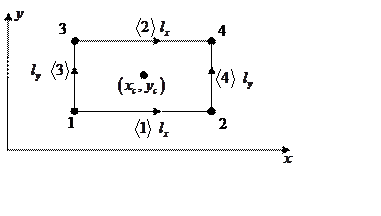
Если каждая сторона элемента определяется постоянной тангенциальной компонентой поля, то поле на элементе можно представить следующим образом:
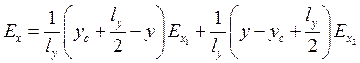
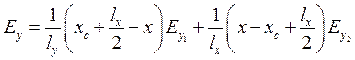
![]() – компонента поля вдоль ребра
– компонента поля вдоль ребра ![]() ,
, ![]() -
компонента поля вдоль ребра
-
компонента поля вдоль ребра ![]() и т. д.
и т. д.
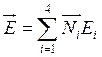 , где
, где ![]() –
тангенциальное поле вдоль ребра
–
тангенциальное поле вдоль ребра ![]() ,
, ![]() - векторные базисные функции, которые
определяются следующим образом:
- векторные базисные функции, которые
определяются следующим образом:
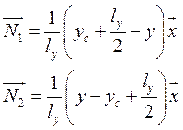
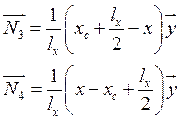
Особенности базисных функций ![]() :
:
Таким образом, мы получили возможность представлять векторные поля там, где нет источника.
![]() ,
, ![]()
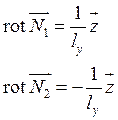
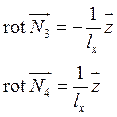
![]() базиса
базиса ![]() –
ненулевые константы.
–
ненулевые константы.
![]() ,
, ![]() .
.
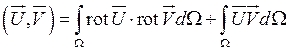 .
.
![]() ,
, ![]()
![]()
![]()
Воспользуемся векторной формулой Грина:
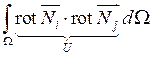 ,
, ![]()
Локальные матрицы:
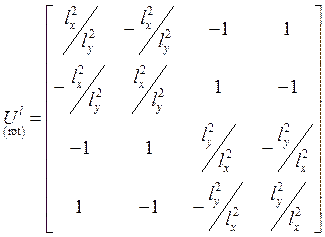 ,
, 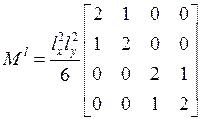 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.