От противного:
Пусть ![]() и
и ![]() – решения
– решения ![]()
![]() и
и ![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.
Обозначим ![]() . Возьмем
. Возьмем ![]() .
.
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() .
.
Предположим, что ![]() решение 2. Найдем
решение 2. Найдем ![]() , что
, что ![]() .
Покажем, что
.
Покажем, что ![]() решение 1.
решение 1.
Пусть ![]() – произвольный элемент
из
– произвольный элемент
из ![]() , тогда
, тогда ![]()
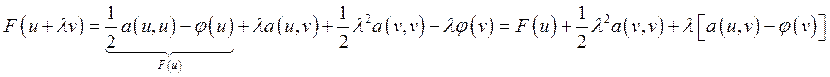
![]()
![]() выполняется для
выполняется для ![]() .
.
Пусть ![]() , т.е.
, т.е. ![]() – решение 1.
– решение 1.
Докажем справедливость 3.
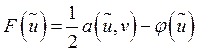
![]() .
.
Выпишем разность
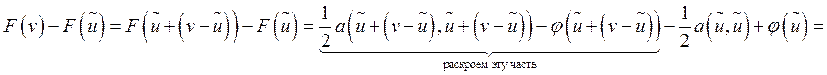
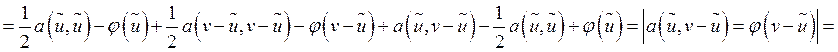
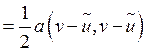 .
. ![]() - решение.
- решение.
Если ![]() – подпространство
– подпространство ![]() , Л.Ф. и Б.Ф.
, Л.Ф. и Б.Ф. ![]() совпадают
с Б.Ф. и Л.Ф. бесконечного пространства
совпадают
с Б.Ф. и Л.Ф. бесконечного пространства ![]() .
.
Рассмотрим эллиптическую краевую задачу и пусть все условия
теоремы Лакса-Мильграма выполнены, т.е. существует ограниченная и коэрцитивная
Б.Ф. ![]() и некоторый ограниченный линейный
функционал, определенный в гильбертовом пространстве
и некоторый ограниченный линейный
функционал, определенный в гильбертовом пространстве ![]() .
.
Решением является единственный элемент ![]() :
:
![]()
![]() (1)
(1)
Если ![]() – симметричная, то
– симметричная, то ![]() (2),
(2), 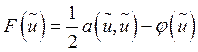 (3).
(3).
Для получения приближенного решения необходимо привести ее
дискретный аналог. В случае метода Ритца означает правильный выбор ![]() -го подпространства
-го подпространства ![]() .
Тогда все условия теоремы выполняются и для
.
Тогда все условия теоремы выполняются и для ![]() .
.
Теорема
Пусть условия теоремы Лакса-Мильграма выполнены и ![]() ,
, ![]() –
гильбертово пространство
–
гильбертово пространство ![]()
![]() элемент
элемент
![]() такой, что
такой, что ![]()
![]() (4). Если
(4). Если ![]() –
симметричная форма, тогда
–
симметричная форма, тогда ![]() (5).
(5).
Теорема не дает процедуры поиска ![]() . Ее
можно получить, построив конечномерное пространство
. Ее
можно получить, построив конечномерное пространство ![]() .
Используя симметричность
.
Используя симметричность ![]() и пусть
и пусть ![]() – некоторый базис
– некоторый базис ![]() ,
т.е. определено множество линейных независимых функций. Тогда каждая функция
,
т.е. определено множество линейных независимых функций. Тогда каждая функция ![]() может иметь единственное представление
может иметь единственное представление 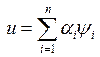 (6),
(6), ![]() .
.
Подставим (6) в (3) и используя свойства Б.Ф. ![]() и
и ![]() ,
получим:
,
получим:
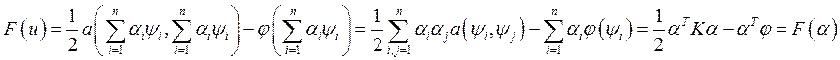 (7)
(7) ![]()
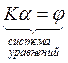 - СЛАУ.
- СЛАУ. ![]() (8)
(8)
![]() – симметричная положительно
определенная матрица и
– симметричная положительно
определенная матрица и ![]() .
.
Т.е. если условие коэрцитивности выполнилось для исходной задачи, то оно будет выполнятся и для дискретной.
Симметричная Б.Ф. ![]() влечет за собой
симметричность матрицы
влечет за собой
симметричность матрицы ![]() .
.
Из теоремы Лакса-Мильграма ![]() Б.Ф.
Б.Ф. ![]() коэрцитивна
коэрцитивна
![]()
![]()
![]() и не зависит от
и не зависит от ![]() . Т.к.
. Т.к. ![]()
![]()
![]() , то справедлива теорема
, то справедлива теорема
Теорема 2
Утверждается, что Б.Ф. ![]() симметрична
и коэрцитивна
симметрична
и коэрцитивна ![]() обеспечивает положительную
определенность матрицы
обеспечивает положительную
определенность матрицы ![]() .
.
Из соотношения (7) ![]()
![]() .
.
![]() – квадратичный функционал в
– квадратичный функционал в ![]() с положительно определенным гессианом,
который минимизируется единственным
с положительно определенным гессианом,
который минимизируется единственным ![]() , которое удовлетворяет
уравнению
, которое удовлетворяет
уравнению ![]() (9).
(9).
Минимизатор ![]() для
для ![]() в
в ![]() определяется
коэффициентом
определяется
коэффициентом ![]() , найденным после решения (9) и его
подстановкой в (6).
, найденным после решения (9) и его
подстановкой в (6).
Для определения ![]() сделаем следующие шаги:
сделаем следующие шаги:
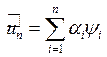 (6).
(6).Выбор базиса целиком определяет вычислительную эффективность всей процедуры решения эллиптической задачи в форме Ритца.
![]() – дифференцируемый оператор.
– дифференцируемый оператор.
В качестве базиса берем собственные функции оператора ![]() . Если Б.Ф. симметрична, то соответствующие
значения
. Если Б.Ф. симметрична, то соответствующие
значения ![]() , удовлетворяющие
, удовлетворяющие ![]() .
Это означает, что они положительны
.
Это означает, что они положительны ![]() и упорядочены
и упорядочены ![]() . Б.Ф. определена
. Б.Ф. определена ![]() в
в
![]()
![]() матрица
матрица ![]()
![]()
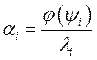
![]() , что с практической точки зрения нереально.
, что с практической точки зрения нереально.
Поэтому пытаемся построить базис. Решаем исходное
операторное уравнение 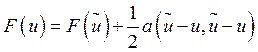
![]() . Из соотношения
. Из соотношения ![]() следует,
что
следует,
что 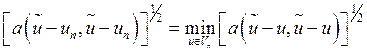 (10) или в энергетической норме это
означает, что
(10) или в энергетической норме это
означает, что ![]() .
.
Фундаментальный результат устанавливает, что метод Ритца
минимизирует ошибку ![]() в энергетической норме на
подпространство
в энергетической норме на
подпространство ![]() . Такая оценка называется оптимальной.
. Такая оценка называется оптимальной.
![]()
![]()
![]() – решение исходной операторной задачи.
– решение исходной операторной задачи.
![]()
![]()
![]()
![]() (11)
(11)
В геометрическом смысле ![]() –
ортогональная проекция по отношения к энергетическому скалярному произведению
–
ортогональная проекция по отношения к энергетическому скалярному произведению ![]() на подпространство
на подпространство ![]() .
.
Используя элементарный Фурье анализ можно найти простое выражение для оценки ошибки (10).
Если базисные функции ![]() пространства
пространства
![]() являются размерно-независимыми и полны в
являются размерно-независимыми и полны в ![]() и ортонормальны по отношению к
энергетическому скалярному произведению
и ортонормальны по отношению к
энергетическому скалярному произведению ![]() , тогда
решение
, тогда
решение ![]() можно представить в виде ряда Фурье:
можно представить в виде ряда Фурье:
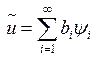
![]()
Если ![]() образовано
образовано ![]() базисными функциями, то сумма
базисными функциями, то сумма 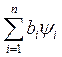 является ортогональной проекцией на
является ортогональной проекцией на ![]() по отношению к энергетическому скалярному
произведению.
по отношению к энергетическому скалярному
произведению.
Т.о. 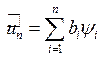 ,
, 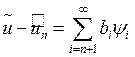 ,
, 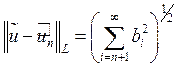 (12).
(12).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.