Методы функционального анализа, страница 6

Метод взвешенных невязок

Метод Галеркина – частный случай обширного класса – метод взвешенных невязок.

Задано (правая часть в операторе)

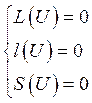 (1)

Пусть  – неточное решение,  – невязка.

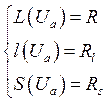 (2)

Введем процедуру нахождения решения.

1. Пусть при  дифференциальное уравнение удовлетворяет точно () – граничный метод.
2. Граничные условия выполняются точно  : ,  – внутренний метод.
3.    – смешанный метод взвешенных невязок.

Введем внутренние скалярные произведения .

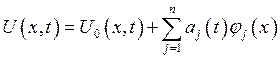 (3)

 – пробные функции.

Это решение – пробное решение. Необходимо найти .

Функция  выбираются так, чтобы начальные и краевые условия удовлетворялись точно (как можно точно). С помощью (3) уравнение  (1) приведем к системе обыкновенных дифференциальных уравнений. Если выбрать коэффициенты [ и ] вместо [ и ], то получим уравнение в частных производных.

Если уравнение (1) стационарное, то  постоянные коэффициенты. Тогда из уравнения (1) получим СЛАУ. Для метода взвешенных невязок внутреннее скалярное произведение   (4). Функции  – весовые или тестовые функции.  должны быть независимыми. Это позволит иметь необходимое число уравнений для определения . Если   полной системе функций, то тогда при  уравнение (4) свидетельствует, что невязка  ортогональна каждому элементу этой полной системы функций. Это означает, что сходимость в среднем . Если сходимость имеет место и представление (3) обеспечивает выполнение точного граничного и начального условий, то ожидаем сходимость  уравнения (1) .

Такую сходимость можно сравнивать с равномерной сходимостью, где .

Выражение (4) слабая форма уравнения (1).

 (5)

Слабую форму можно записать в дискретном виде: 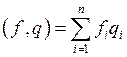 (6)

Это позволит перейти к дискретному методу взвешенных невязок. Использование численного интегрирования уравнения (4) – это дискретный аналог метода взвешенных невязок.

Метод коллокаций

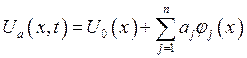
Отличие этого метода: в качестве тестовых функций задаются - функции Дирака: ,   .

В этом случае все невязки вычисляем в нулях полинома Чебышева .

Здесь использовано минимаксное свойство полинома Чебышева.

Пробные функции выбираются любыми.

Метод наименьших квадратов

В качестве тестовых функций используются 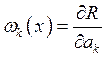, где  – неизвестные коэффициенты, подлежащие определению.

Выбор  в такой форме эквивалентен выбору : .

Метод моментов

,

Аппроксимация (лекция 10.04.04)

1.  Сетка

2.  Свойства и качества дискретной системы

3.  Порядок аппроксимации

Пусть задана  в . Ищем конечномерный аналог и аппроксимацию.

 - гладкая функция, определенная , .

Пусть  - пространство узловых КЭ, натянутых на , т.е. каждой функции  соответствует некоторый узел  и такая производная , что выполняется:

                                                      

Пространство  будет иметь такую степень, что любой полином степени  можно представить в полной комбинации базисных функций (полная степень полинома). . Например, полная степень многочлена  равна 3, , т.е. степень пространства  будет равна 4.

 - полином, ему соответствует некоторая комбинация .

В весовые коэффициенты  будут равны .

Определим степень пространства S.

Узловые производные  должны иметь порядок .

1.  Для линейной:

2.  Для кубической:

и т. д.     

Определим порядок аппроксимации, который может быть достигнут в пространстве  степени . Область  разбита на КЭ . КЭ характеризуется геометрическими свойствами: , .

В скалярных задачах: гладкая функция – решение дроблением сетки.

В векторных: дробление сетки физически не обосновано -  не дает верного решения.

Цель: исследовав последовательность узловых подпространств, установить зависимость ошибки аппроксимации  как функции параметра .

Введем понятие однородности. Базисные функции  имеют однородность порядка  при условии, что существуют такие , что  справедливо: