Методы функционального анализа

Конечно-разностная схема для аппроксимации ДУ в частных производных................. 2

Одношаговые явные схемы. Чехарда со средних точек..................................................... 3

Метод Фон Неймана........................................................................................................... 3

Классификация разностных схем................................................................................. 4

Схема с весами................................................................................................................ 5

Конформный МКЭ.................................................................................................................. 6

Теорема Лакса-Мильграма................................................................................................ 6

Метод Ритца........................................................................................................................ 8

Анализ погрешности метода Ритца.............................................................................. 8

Метод Галеркина. Некоэрцитивная проблема.................................................................. 10

Классификация сеток....................................................................................................... 11

Классическое представление метода Галеркина.............................................................. 12

Понятие распределения................................................................................................... 12

Метод взвешенных невязок............................................................................................. 13

Метод коллокаций............................................................................................................ 14

Метод наименьших квадратов........................................................................................ 14

Метод моментов............................................................................................................... 14

Аппроксимация (лекция 10.04.04)...................................................................................... 14

Метод Галеркина для параболических уравнений........................................................... 15

Обобщенная проблема собственных значений................................................................. 17

Однородный волновод...................................................................................................... 17

Метод конечных объемов.................................................................................................... 19

Векторный МКЭ (лекция 08.05.04)................................................................................. 20

Методы решения СЛАУ в подпространстве Крылова...................................................... 22

Проекционные методы..................................................................................................... 22

Векторный МКЭ. Общее представление............................................................................ 22

Конечно-разностная схема для аппроксимации ДУ в частных производных

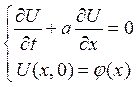     (1) - задачи Коши

 - аналитическое решение,  - линеаризованная скорость конвекции.

Конечно – разностный метод называется консервативным, если он обеспечивает выполнение определённых интегральных законов сохранения, справедливых для данного уравнения.

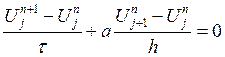    (2)

 - задано

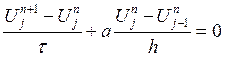
(3) - схема Годунова

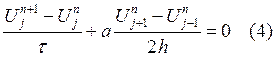
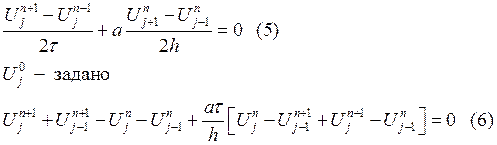
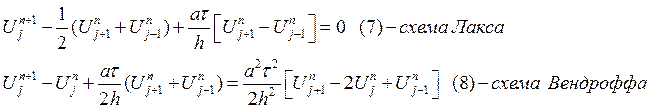
Найдем порядок аппроксимации для схемы (3)

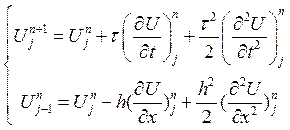   подставим в (3), получим:

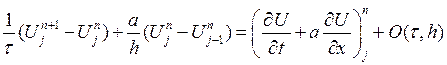
Схема Годунова аппроксимирует (1) с первым порядком по

Устойчивость схемы 3

Из рисунка видно, что положение точки  соответствует схеме Годунова только при условии 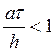  - условие сходимости Куранта.

Но: Положение точки Р никогда не соответствует схеме (2)

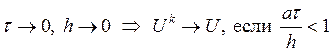,  - число Куранта.

Одношаговые явные схемы. Чехарда со средних точек.

Аппроксимируем уравнение (1) схемой (5), которая имеет второй порядок аппроксимации и по времени и пространству. Это означает, что вычисление значения на  слое возможно при известных значениях на  и   слое – это явная одношаговая трехслойная схема.

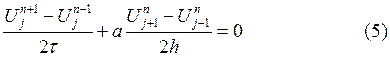
Необходимо отметить, что каждое новое значение  на четном временном слое вычисляется как величина на предыдущем четном временном слое плюс некоторая добавка, а предыдущий нечетный временной слой «перепрыгивается».

Метод Фон Неймана         

Исследуем на устойчивость (5)

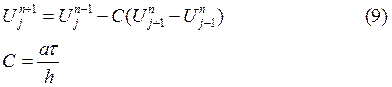
Каждую компоненту представим её Фурье-образом

Подставим (11) в (9), получим:

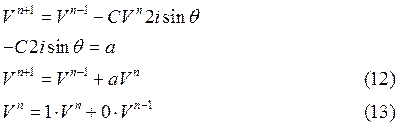
Из (12) и (13) выпишем систему уравнений

Условие устойчивости, согласно методу ФН определяется следующим образом:

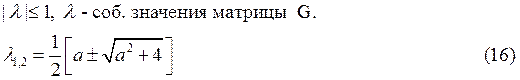
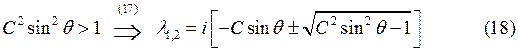
Абсолютная величина  будет больше 1 - это означает неустойчивость схемы (5)

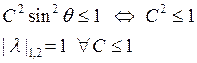   - условие устойчивости

Условие , в котором конвекция , невыполняется , т.е. решение не затухающее произвольное начальное приближение просто сдвигается со скоростью конвекции, равной . Это означает, что

Таким образом, метод Фон Неймана показывает, что схема «Чехарда» правильно моделирует одно из главных свойств, присущих уравнению (1), а именно, отсутствие затухания при .