Оценка ошибки в норме ![]()
Т.к. Б.Ф. ![]() удовлетворяет условиям
теоремы Лакса-Мильграма
удовлетворяет условиям
теоремы Лакса-Мильграма ![]() существуют такие
константы
существуют такие
константы ![]() и
и ![]() , что
, что ![]()
![]() . Тогда (10) можно
представить в виде
. Тогда (10) можно
представить в виде ![]()
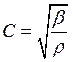 (13).
(13).
Оценка (13) почти оптимальная. Этот результат приводит к
проблеме аппроксимации: Как хорошо можно приблизить функцию из ![]() функцией из
функцией из ![]() в норме
в норме
![]() (
(![]() )?
)?
Т.к. для краевых задач порядка ![]() норма
норма ![]() – это соболевская норма
– это соболевская норма ![]() , то можем получить оценку погрешности и в
норме
, то можем получить оценку погрешности и в
норме ![]() .
.
Формулировка несимметричной вариационной задачи
Пример:
![]() в
в ![]() ,
, ![]() .
.
Пусть ![]()
![]()
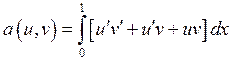 ,
, ![]() .
.
Дано: ![]() . Найти
. Найти ![]() такое, что
такое, что ![]()
![]() .
.
Доказать, что ![]() – непрерывно.
– непрерывно.
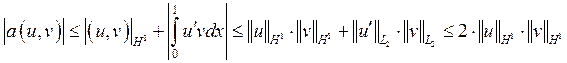
следовательно, ![]() непрерывно с const=2.
непрерывно с const=2.
Докажем, что ![]() коэрцитивно.
коэрцитивно.
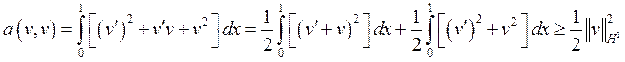
следовательно, ![]() коэрцитивно с const=1/2.
коэрцитивно с const=1/2.
Это означает, что для симметричного случая будет существовать единственное решение.
Пусть Б.Ф. ![]() некоэрцитивна, но
удовлетворяет слабому неравенству (аналог условия 3 в теореме Л..-М..).
некоэрцитивна, но
удовлетворяет слабому неравенству (аналог условия 3 в теореме Л..-М..).
Необходимо ввести дополнительные условия:
![]()
![]() .
.
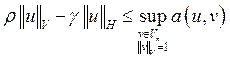
![]() и
и ![]() не зависят от решения.
не зависят от решения.
Теорема 4
Пусть ![]() и пусть рассматривается
задача нахождения
и пусть рассматривается
задача нахождения ![]() такая, что Б.Ф.
такая, что Б.Ф.
![]()
![]() (1)
(1)
Если условия 1-4 выполнены, то существует целое ![]() такое, что (1) имеет единственное решение
такое, что (1) имеет единственное решение ![]()
![]() , кроме того,
, кроме того, ![]() , независящая от
, независящая от ![]() и
и
![]() , что
, что ![]() и
и ![]() . Это справедливо для
. Это справедливо для ![]() .
.
Конформный МКЭ – это метод, для которого ![]() (
(![]() ) есть
подпространство
) есть
подпространство ![]() , а Б.Ф. и Л.Ф. дискретной задачи
совпадают с соответствующими формами исходной задачи.
, а Б.Ф. и Л.Ф. дискретной задачи
совпадают с соответствующими формами исходной задачи.
Дифференциальная задача:
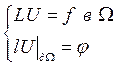
![]()
![]()
![]() – сеточный аналог. Для
определения сетки необходимо определить признак соседства:
– сеточный аналог. Для
определения сетки необходимо определить признак соседства:
соседними являются элементы, если они имеют общими узел/ребро/грань. Иначе не являются соседними.
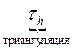 ,
, Структурированная сетка
Сетка, у которой предопределенная структура или порядок
всегда существует. В двумерной области сетка структурирована логически, если
точки ![]() и
и ![]() –
соседи относительно точки
–
соседи относительно точки ![]() . Предполагается, что
эта логическая структура соблюдается для всех точек области и неявно
используется при конструировании конечномерной системы алгебраических уравнений,
описывающих соответствующий объект. Структурированные сетки формируют семейство
четырехугольных сеток, которые используются в численных методах, т.к. соседние
точки связаны в пути, то добавление или исключение точек, требует
переиндексирования всех точек.
. Предполагается, что
эта логическая структура соблюдается для всех точек области и неявно
используется при конструировании конечномерной системы алгебраических уравнений,
описывающих соответствующий объект. Структурированные сетки формируют семейство
четырехугольных сеток, которые используются в численных методах, т.к. соседние
точки связаны в пути, то добавление или исключение точек, требует
переиндексирования всех точек.
Неструктурированная сетка
Сетки, не имеющие предопределенной логической структуры, и
поэтому содержат систему произвольно расположенных точек. Единственный сеточный
индекс достаточен, чтобы идентифицировать точку (индекс признак соседства не
определяет). Сеточные точки не лежат вдоль некоторого конкретного направления.
Они произвольно разбросаны по области. Соседние точки связаны отрезками.
Сеточные точки ![]() формируют вершины треугольника,
отрезки их соединения – ребра.
формируют вершины треугольника,
отрезки их соединения – ребра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.