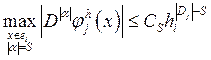Методы функционального анализа, страница 7

                                             где 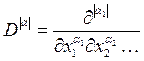, , и это выполняется вплоть до порядка .

 - порядок производной, интерполируемой базисной функцией  функции в узле  базисной функции.

Соотношение позволяет определить качество аппроксимации в геометрических характеристиках сетки. Переход от одной сетки к другой характеризуется якобианом.

Коэффициент  отвечает за геометрические свойства сетки.

Рассмотрим линейные функции на треугольнике.

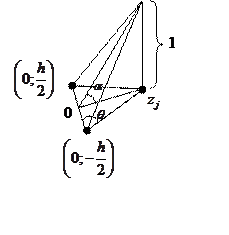Значение функции в  равно 1, в остальных – 0. Всегда .

Для  . Возьмем производную: .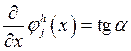

.

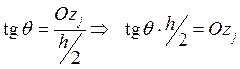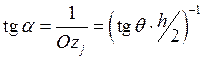
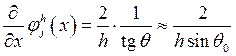; При разбиении .

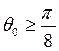При  , .

Метод Галеркина для параболических уравнений

,

                                                  

                                                       

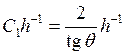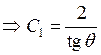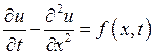
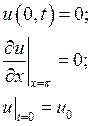
Оператор не самосопряженный, поэтому решаем методом Галеркина.

,

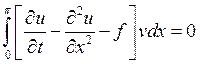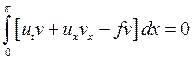, . Переменная  в такой форме – непрерывна.

,

,

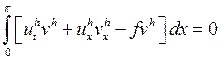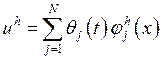
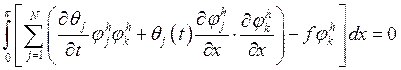Получаем задачу Коши.

.  – матрицы массы и жесткости соответственно.

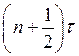,  - шаг по времени.

Схема Кранка-Николсона:

Выписывается симметрично относительно половины шага и имеет 2-ой порядок аппроксимации по времени.

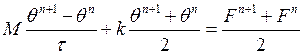
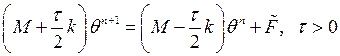 Матрица СЛАУ  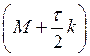положительно определена.

Погрешность: .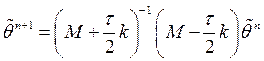

Спектральный радиус матрицы 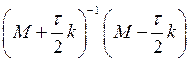  должен быть меньше 1.

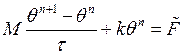
,  аппроксимируем, чтобы не решать СЛАУ на каждом шаге по времени.

Диагонализируем матрицу  в . Пусть  - диагональная матрица.

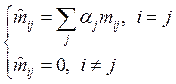
Это интеграл в слабой форме, который аппроксимируется законом средней точки.

Для прямоугольной равномерной сетки .  равен строковой сумме элементов матрицы М.

Диагонализированная матрица на диагонали должна иметь положительные элементы.

Домашняя работа: сделать то же самое для неявной схемы.

Неявная схема:

,   .

Обобщенная проблема собственных значений

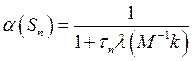
(лекция 24.04.04)

Исходная задача:

- тождественный оператор

Найти собственные значения  и принадлежащие им собственные  функции

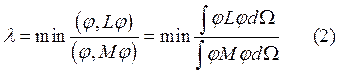
Рассмотрим скалярное уравнение Гельмгольца. Оно описывает электромагнитное поле.

   в              (3)

, , , граница , - соответствующее собственное значение.

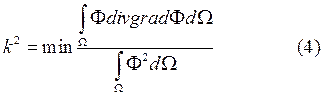
Воспользуемся формулой Остроградского-Гаусса

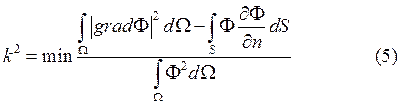
Введем граничные условия:

1. Условия Дирихле            

(Если мы решаем проблему собственных значений, краевые условия будут однородны)

2. Условие Неймана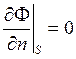            

Для условий Дирихле и Неймана (5) будет иметь вид

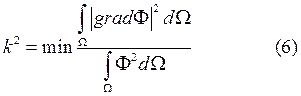
3. Третьи краевые условия 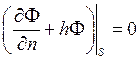         (5) будет иметь вид

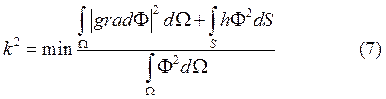
Решить задачу (1) можно различными способами. Например, выбираем некоторое пространство решений (его базис): . Пространство выбираем таким образом, чтобы базисные функции удовлетворяли краевым условиям нашей задачи.

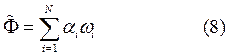
Ищем решение в виде (8). Вариационные постановки для решения спектральных проблем могут быть использованы в следующих приложениях:

- расчет критической частоты волновода

- постоянное распространение волн

- резонансная частота резонатора.

Однородный волновод

В однородных волноводах есть два множества различных мод.

Одно множество мод не имеет компонент магнитного поля в направлении распространения магнитного поля. Такой режим называется поперечная магнитная мода или ТМ-мода.

Второе множество не имеет компонент электрического поля в направлении распространения поля. Оно называется поперечным электрическим или ТЕ-мода.

Пусть - направление распространения поля. Под полем подразумевается напряженность, т.е. , а под индукцией . Тогда будем рассматривать  – частота.

В направлении распространения волны происходит изменение ее амплитуды – затухание. Коэффициент затухания обозначим

  Получим два однотипных уравнения относительно компонент  и . Обозначим любую из них за

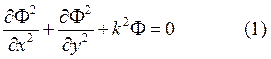
, диэлектрическая проницаемость, - магнитная проницаемость.

ТЕ и ТМ отличаются условиями на границе.

   

   

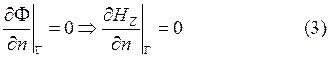
Для задачи (1), (2), (3) сформулируем вариационную постановку (оператор симметричный, положительно определенный) в форме Ритца.

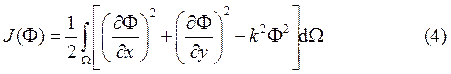
 - поперечное сечение волновода.