Выпишем конечно-элементную аппроксимацию для решения (4).
Определим конечномерное пространство ![]() . В качестве конечных
элементов возьмем кусочно-линейные функции на треугольниках. В результате
получим
. В качестве конечных
элементов возьмем кусочно-линейные функции на треугольниках. В результате
получим
![]() , где матрица
, где матрица ![]() ассемблирована из
следующих элементов:
ассемблирована из
следующих элементов:
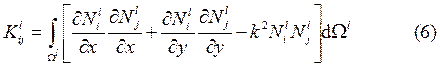
Нам неизвестно ![]() . Выпишем задачу
относительно
. Выпишем задачу
относительно ![]() . Представим элементы локальной матрицы
следующим образом:
. Представим элементы локальной матрицы
следующим образом:
![]()
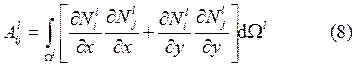
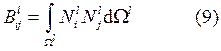
Получим, что (5) можно представить в виде
![]()
Получим обобщенную проблему собственных значений
![]() -симметричные разреженные
матрицы,
-симметричные разреженные
матрицы, ![]() - положительно определенная.
- положительно определенная.
Решив (10) найдем ![]() . Будем задавать частоту
. Будем задавать частоту
![]() и свойства материала
и свойства материала ![]()
![]() получим коэффициент
затухания
получим коэффициент
затухания ![]() .
.
![]() . Матрица
. Матрица ![]() очень
мешает, ее надо убрать. Найдем
очень
мешает, ее надо убрать. Найдем ![]() . Т.к.
. Т.к. ![]() - симметричная и положительно определенная,
то
- симметричная и положительно определенная,
то ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Это энергетически сбалансированные методы.
![]() ,
, ![]() - поток
поля
- поток
поля ![]() через поверхность
через поверхность ![]() ,
ограничивающую область
,
ограничивающую область ![]()
Метод конечных объемов является наиболее эффективным в следующем случае:
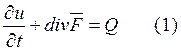
![]() заданная векторная функция,
которая называется векторным потоком.
заданная векторная функция,
которая называется векторным потоком.
![]() - источник излучения, который
возможно является функцией пространства и времени.
- источник излучения, который
возможно является функцией пространства и времени.
Умножим обе части (1) на тестовую функцию ![]() и проинтегрируем.
и проинтегрируем.
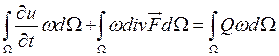
![]()
Воспользуемся формулой интегрирования по частям.
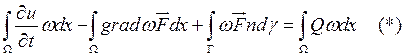
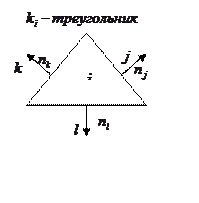 Определим контрольный объем. Например, в качестве контрольного
объема возьмем треугольник.
Определим контрольный объем. Например, в качестве контрольного
объема возьмем треугольник.
В качестве тестовой функции ![]() для МКО
используется функция, равная единице на контрольном объеме и нулю вне его.
Тогда в левой части уравнения (*) интеграл
для МКО
используется функция, равная единице на контрольном объеме и нулю вне его.
Тогда в левой части уравнения (*) интеграл
![]()
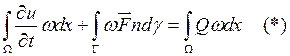
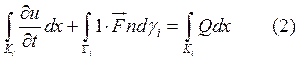
Мы получили основное выражение для конечно-объемных
формулировок задачи (1). Определим функцию ![]() , чтобы
упростить формулировку:
, чтобы
упростить формулировку:
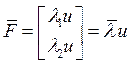
![]()
![]()
Необходимо отметить, что правую часть (2) тоже можно определить приближенно.
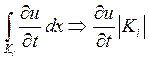 ,
, 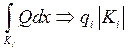
Тогда конечно-объемное уравнение (2) имеет вид:
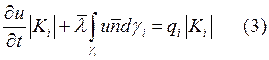
Интеграл 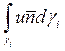 сумма интегралов по
ребрам контрольного объема (треугольника). Пусть
сумма интегралов по
ребрам контрольного объема (треугольника). Пусть ![]() - номер
ребра. Величина
- номер
ребра. Величина ![]() аппроксимируется
аппроксимируется ![]() . Через
. Через ![]() обозначим
длину каждого ребра. Введем следующие обозначения:
обозначим
длину каждого ребра. Введем следующие обозначения:
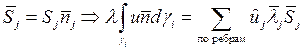
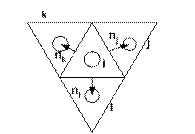
Пусть соседними треугольниками являются треугольники ![]() . Контрольный объем, который мы
рассматриваем, ассоциирован с узлом
. Контрольный объем, который мы
рассматриваем, ассоциирован с узлом ![]() . Величина
. Величина ![]() может быть определена достаточно просто:
может быть определена достаточно просто: 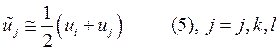
В результате получим
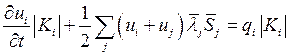
![]() , т.к. сумма всех входящих и
выходящих потоков должна быть скомпенсирована.
, т.к. сумма всех входящих и
выходящих потоков должна быть скомпенсирована.
![]()
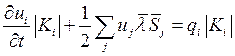
Суммирование производится по всем соседним ячейкам.
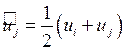
![]() -ориентирован
относительно нормали
-ориентирован
относительно нормали ![]() , где
, где ![]() -длина
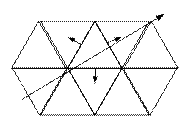
ребра. Скалярный МКЭ работает с узловыми значениями функций, МКО работает с
потоками входящими -выходящими в(из) объема.
-длина
ребра. Скалярный МКЭ работает с узловыми значениями функций, МКО работает с
потоками входящими -выходящими в(из) объема. 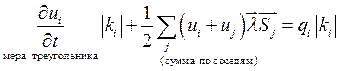
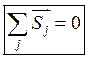
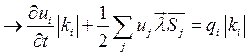 суммирование
по всем соседним ячейкам.
суммирование
по всем соседним ячейкам.
 Векторный МКЭ (лекция 08.05.04)
Векторный МКЭ (лекция 08.05.04)В простых аппроксимациях возникает следующая проблема: их
невозможно использовать при больших ![]() . В МКО типичным
является использование в этом случае противопотоковых схем: модифицируем
соотношение
. В МКО типичным
является использование в этом случае противопотоковых схем: модифицируем
соотношение 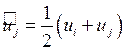 .
.
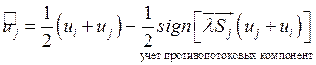 . С учетом этого соотношения
получаем
. С учетом этого соотношения
получаем 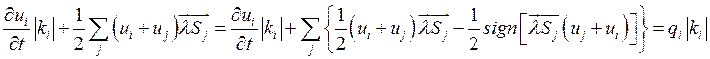
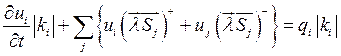
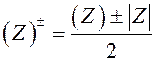
Для ячейки ![]() , получаем:
, получаем:
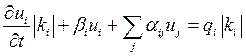
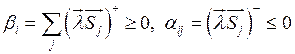
Когда можно сказать, что мы построили решение с нужным порядком аппроксимации и правильное решение получили при дроблении сетки.
Мы получили, что диагональные элементы должны быть не отрицательны.
Не диагональные элементы – не положительны.
Строчные суммы элементов = 0. Получили матрицу, обладающую свойством слабого диагонального преобладания. Неполные объемы (краевые условия) – слабое диагональное преобладание. В качестве КО используется триангуляция.
МКР
МКО ![]()
МКЭ![]()
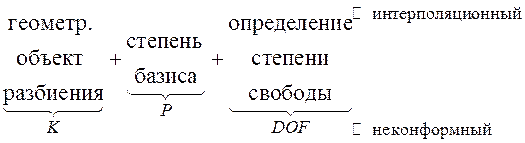
Строим барицентры на пересечении медиан

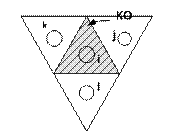
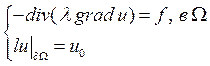
Численное решение этой краевой задачи:
1.
Построим дискретный аналог области ![]() (не пересекающиеся треугольники)
(не пересекающиеся треугольники)
2. Строим КО
3.
Делаем предположение о том, что представляет собой профиль функции u (линейная, квадратичная) + предположение о коэффициенте ![]() .
.
![]()
Будем полагать, что узлы, в которых неизвестные значения функции совпадают с узлами сетки
![]()
![]()
![]() -тестовая функция. Если выбрать
последовательность функций
-тестовая функция. Если выбрать
последовательность функций ![]() , то получим количество
уравнений достаточное для определения решений.
, то получим количество
уравнений достаточное для определения решений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.