Пусть ![]() – число вершин,
– число вершин, ![]() – число ребер,
– число ребер, ![]() – число
треугольников.
– число
треугольников.
![]() .
.
С каждым треугольником ![]() будем
связывать точку
будем
связывать точку ![]() , которая определяет
положительность треугольника в
, которая определяет
положительность треугольника в ![]() . Определение
. Определение ![]() не является единственным. Определим ребра
треугольников, как ориентированные отрезки, соединяющие точки
не является единственным. Определим ребра
треугольников, как ориентированные отрезки, соединяющие точки ![]() и
и ![]() .
.
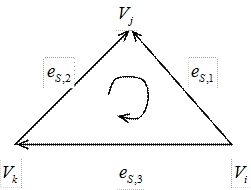 Вектор, соединяющий
Вектор, соединяющий ![]() и
и ![]()
![]() .
.
Пронумеровать ребра и их ориентацию определить.
Каждое ребро принадлежит треугольнику ![]() , которое лежит слева от него и
треугольнику
, которое лежит слева от него и
треугольнику ![]() , который лежит справа от него. С каждым
ребром можно ассоциировать единичный тангенциальный вектор
, который лежит справа от него. С каждым
ребром можно ассоциировать единичный тангенциальный вектор 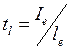 ,
, ![]() – длина
ребра. Можно определить единичный вектор нормали
– длина
ребра. Можно определить единичный вектор нормали ![]() .
Необходимо задать обход области (по часовой стрелке).
.
Необходимо задать обход области (по часовой стрелке).
Такие структуры данных образуются посредством обработки первичной (список сеточных элементов) и вторичных (определяет связи между элементами первичной сетки) структур данных.
Пример для двумерного случая: первичная содержит список треугольников, вершин и ребер. Вторичная содержит перекрещивающиеся индексы. Массив индексных ребер определяется номерами ячеек слева и справа от ребра. Остальные массивы индексных ячеек определяется индексами 3х вершин и 3х ребер.
Не все классические постановки оказываются правильными. Существуют задачи, где разрывное решение, правая часть – поэтому необходимо искать обобщенное решение (основатель Дирак).
Пример.
Пусть некоторая материальная точка имеет массу =1 и совпадает с началом координат.
Нужно распределить эту массу равномерно по шару ![]() . Определим плотность
. Определим плотность 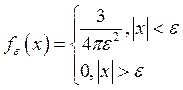 .
.
В качестве искомой плотности ![]() примем поточечный
предел последовательности
примем поточечный
предел последовательности ![]() ,
, ![]() :
:
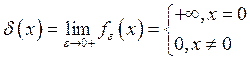 (*).
(*).
Потребуем от ![]() , чтобы
, чтобы ![]() давал массу вещества, заключенную в этом
объеме:
давал массу вещества, заключенную в этом
объеме:
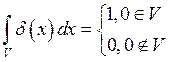 (**).
(**).
В силу (*) левая часть (**) всегда равна нулю. Это
противоречие показывает, что поточечный ![]() не
может быть взят в качестве плотности
не
может быть взят в качестве плотности ![]() .
.
Введем понятие и вычислим слабый предел. Для любой непрерывной
функции ![]() найдем предел числовой последовательности
найдем предел числовой последовательности ![]()
![]() . Покажем, что этим
пределом является функционал
. Покажем, что этим
пределом является функционал ![]() , который сопоставляет
каждой непрерывной функции
, который сопоставляет
каждой непрерывной функции ![]() число
число ![]() .
.
![]() – это определение плотности
– это определение плотности ![]() или известная функция Дирака.
или известная функция Дирака.
Для приложения функционального анализа в физике необходимо обобщить классическое понятие функции так, как это сделал Дирак, а обосновал Лоран Шварц.
Теория распределения – это теория обобщенных функций.
Интеграл Римана позволяет подчеркнуть связь между распределениями и обобщенными функциями.
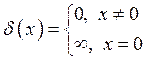 ;
; 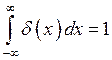
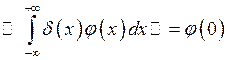 (1)
(1)
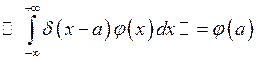 (2)
(2)
![]() вводится так, чтобы можно было
выполнить интегрирование по частям
вводится так, чтобы можно было
выполнить интегрирование по частям
![]() :
: 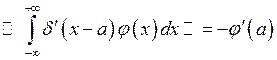 (3)
(3)
Это выполняется ![]() дифференцируемой
функции
дифференцируемой
функции ![]() .
.
Есть функция ![]() – кусочно-непрерывная
(не обязательно дифференцируемая в обычном смысле), то ее производная в
обобщенном смысле определяется как такая
– кусочно-непрерывная
(не обязательно дифференцируемая в обычном смысле), то ее производная в
обобщенном смысле определяется как такая ![]() :
: 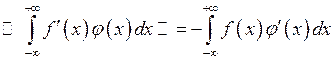 (4)
(4)
Это справедливо ![]()
![]() непрерывной
дифференцируемой при
непрерывной
дифференцируемой при ![]() , которая тождественно обращается
в нуль вне некоторого конечного интервала.
, которая тождественно обращается
в нуль вне некоторого конечного интервала.
![]() и
и ![]() определяются
не заданием их значений для каждого значения
определяются
не заданием их значений для каждого значения ![]() , а значениями
интегралов
, а значениями
интегралов ![]() , причем это определено
, причем это определено ![]()
![]() из некоторого наперед
выбранного класса.
из некоторого наперед
выбранного класса.
Это означает, что (1)-(2)-(3)-(4) линейно зависят от функции
![]() .
.
Тогда обобщенная функция – это линейный функционал, определенный на выбранном надлежащим образом классе пробных функций.
Различные классы пробных функций порождают различные классы
распределений. Чтобы охватить широкий класс пробные функции ![]() должны быть бесконечно дифференцируемы и
каждая из них должна обращаться в нуль вне некоторого промежутка. Они образуют
класс
должны быть бесконечно дифференцируемы и
каждая из них должна обращаться в нуль вне некоторого промежутка. Они образуют
класс ![]() . Соответствующие функции
. Соответствующие функции ![]() образуют класс
образуют класс ![]() .
Носителем функции
.
Носителем функции ![]() называют замыкание тех точек
называют замыкание тех точек ![]() , для которых
, для которых ![]() .
.
Условие, которое выделяет распределения из множества всех
линейных функционалов следующее: если определена сходимость ![]() пробных функций, то функционал
пробных функций, то функционал ![]() будет непрерывным относительно этой
сходимости
будет непрерывным относительно этой
сходимости ![]()
![]() при
при ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.