Методы функционального анализа, страница 2

Рассмотрим устойчивость разностной схемы. Для стационарной задачи это возможно исследовать только по правой части, а не по начальным данным.

Сеточная функция - конечномерное подпространство.

Предположим, что (1) однозначно разрешима =>

Введем в рассмотрение скалярное произведение  и порожденную им норму

, тогда - решение задачи (1) будет удовлетворять любому из следующих тождеств:

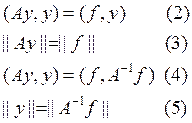 - априорные оценки

Из этих тождественных соотношений можно получить норму решения  через правую часть (1) – априорная оценка. Для этого нужно предположить свойства оператора :

Пусть оператор А положительно определен  из (2) и из неравенства Коши-Буняковского

      

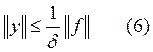
Пусть известно точное решение и приближённое решение:

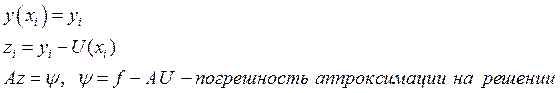
(Если оператор  - линейный).

Пусть задача (1) устойчива, т.е. выполнена оценка (6), тогда справедливо следующее:

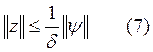
Оценка (7) свидетельствует о том, что имеет место сходимость нашей задачи тогда и только тогда, когда  при .

Для исследования сходимости необходимо доказать устойчивость и проверить стремление к нулю . В зависимости от того, какая задача и какое пространство, будут получены разные оценки.

(Для положения определения спектров обычно используют энергетические нормы).

Классификация разностных схем

если , то из этого соотношения (), получаем двухслойную схему

.

Если , то схема трехслойная

Любую двухслойную схему можно записать в виде

,

,

,

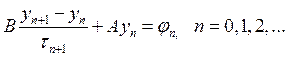
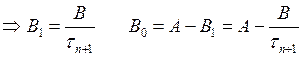,  - тождественный оператор  схема явная.

Схема с весами

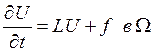
 - задано

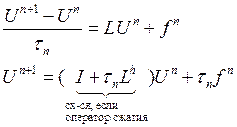
, где  - вес.

Исследование на устойчивость.

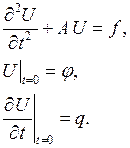
Будем полагать, что оператор  не зависит от времени.

Запишем РС, аппроксимирующую это уравнение со вторым порядком по :

                                                                                    (*)

,

.

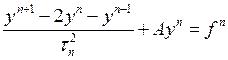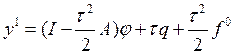Исследуем на устойчивость спектральным методом:

Пусть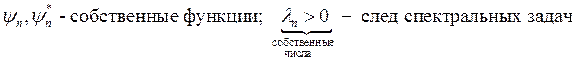

;  одно и то же, так как  .

Пусть  образуют базис, тогда решение уравнения можно искать в виде:

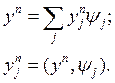
Подставим в (*) и умножим на , то для коэффициентов ряда Фурье  получим уравнение:

.

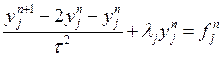Общее решение соотношения можно искать в виде:

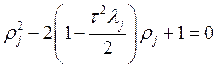
корни должны быть комплексно–сопряжёнными и .

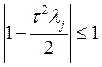
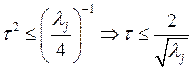
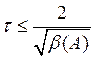  , где  - верхняя граница спектра .

Если  - симметричная и положительно определённая, то .

Конформный МКЭ

Пусть  – открытое подмножество в  с кусочно-гладкой липшецкой границей.  – пространство кусочно-интегрируемых в смысле Лебега функций на .

Определение. Функция , имеет слабую производную  в  при условии, что  и  – бесконечно дифференцируемая функция, не обращающаяся в ноль только на компактном множестве .

 приводит к формуле Грина интегрирования по частям.

Если вторая производная существует и совпадает со слабой  слабая производная существует.

Концепция слабых производных приводит и к другим дифференцируемым операторам.

Пусть  – векторная функция, которая определяет поле.

Тогда  есть  в слабом смысле и это приводит к  .

Пусть  – гильбертово пространство со скалярным произведением и порождает норму  .

Введем в рассмотрение Б.Ф. . Она обладает свойствами:

1.   .
2. 
3.  - ограниченность.
4. , ,  не зависит от  - коэрцитивность.

Симметричность:  .

Введем линейную форму: .

Свойства:

5.   .
6.   .

5, 6 определяют линейный ограниченный функционал.

Теорема Лакса-Мильграма

Пусть  – вещественное векторное пространство,  – Б.Ф.  симметрична и положительно определена ().

 – линейная форма.

Пусть  – квадратичная форма .

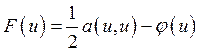Рассмотрим задачи:

1. Найти такое , что  .
2. Найти . что  .

Тогда

1. каждая из задач имеет не более 1 решения.
2. если одна из задач допускает некоторое решение, то и другая допускает тоже самое решение.
3. если  – решение, то   равно .

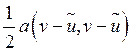Теорема говорит о том, что в случае симметричного и положительно определенного оператора методы Ритца и Галеркина дают одно и тоже решение.

Доказательство:

Задача 1 имеет единственное решение.