Измерительные медицинские системы. Источники погрешностей при аппаратурных измерениях в медицине, страница 18

Коэффициенты  называют нагрузкой i-й переменной на j-й фактор или нагрузкой j-го фактора на i-ю переменную. В самой простой модели факторного анализа считается, что факторы  взаимно независимы и их дисперсии равны единице, а их случайные величины  тоже независимы друг от друга и от какого-либо фактора .

Максимально возможное количество факторов  при заданном количестве признаков  определяется неравенством:

,                                                             (9.4)

Неравенство (9.4) должно выполняться, чтобы задача не вырождалась в тривиальную. Данное неравенство получается на основании подсчета степеней свободы, имеющихся в задаче. Сумму квадратов нагрузок в выражении (9.4) называют общностью соответствующего признака , и чем больше это значение, тем лучше описывается признак  выделенными факторами . Общность есть часть дисперсии признака, которую объясняют факторы. В свою очередь,  показывает, какая часть дисперсии исходного признака остаётся необъяснённой при используемом наборе факторов, и данную величину называют специфичностью признака. Таким образом, дисперсия признака = общность 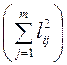 + специфичность .

Из соотношения (9.4) следует, что коэффициент корреляции любых двух признаков  и  можно представить суммой произведений нагрузок некоррелированных факторов:

.                                          (9.5)

Задача факторного анализа не имеет однозначного решения. Равенства (9.4) не поддаются непосредственной проверке, т. к.  исходных признаков задаётся через  других переменных – простых и специфических факторов. Поэтому представление корреляционной матрицы факторами, как говорят, ее факторизацию, можно произвести бесконечно большим числом способов.

На практике обычно поступают следующим образом. Вычисления начинают с  (однофакторная модель). Затем проверяют, насколько корреляционная матрица, восстановленная по однофакторной модели в соответствии с основным соотношением факторного анализа (9.5), отличается от корреляционной матрицы исходных данных. Если однофакторная модель признается неудовлетворительной, испытывается модель с  и т. д. до тех пор, пока при некотором  не будет достигнута адекватность или число факторов  в модели не превысит максимально допустимое. В последнем случае говорят, что адекватной модели факторного анализа не существует.

Если факторная модель существует, тогда производят вращение полученной системы общих факторов, т. к. полученное решение есть лишь одно из возможных. Вращение может производиться с учетом достижения тех или иных целей.

Например, таким образом, чтобы как можно большее число факторных нагрузок стало нулями, и каждый фактор по возможности описывал группу сильно коррелированных признаков – так поступают наиболее часто. Также можно исходить из получения содержательной интерпретации факторов. Например, можно потребовать, чтобы исчезли какие-то трудно интерпретируемые признаки. Или чтобы один фактор был нагружен преимущественно признаками одного типа, а другой – признаками другого типа. На рис. 9.19 приведена схема исследовательской стратегии Р. Кэттела.

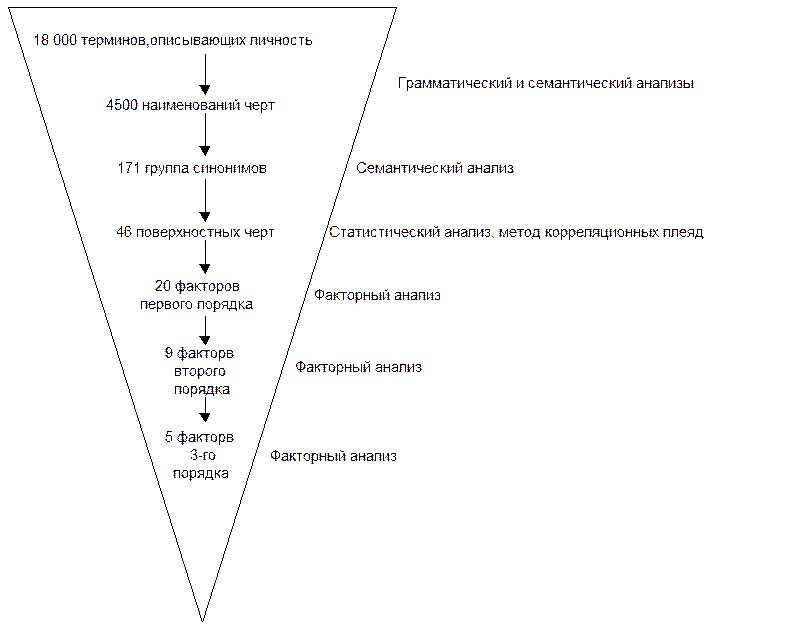
Рис. 9.19 – Схема исследовательской стратегии Р. Кэттела

В заключение всей процедуры факторного анализа с помощью математических преобразований выражают факторы  через исходные признаки, то есть получают в явном виде параметры линейной диагностической модели. Примером применения факторного анализа в психологии являются результаты, полученные при разработке 16-факторного личностного опросника [19].

Контрольные вопросы

1. Можно ли рассматривать процесс медицинской диагностики как измерительную задачу?

2. В чем отличие медицинских шкал от шкал, используемых в технике.

3. В чем разница между медицинскими данными и медицинскими показателями?

4. Перечислите шкалы, используемые в медицине.

5. В чем отличие обычного измерения от комплексного измерения?