Измерительные медицинские системы. Источники погрешностей при аппаратурных измерениях в медицине, страница 17

Таким образом, потенциальная возможность двоякой трактовки величин, образующих диагностическую цепочку (цепочку правил продукции «ЕСЛИ-ТО»), следует из того обстоятельства, что формально определения классов и признаков совпадают: в обоих случаях речь идет о величинах, используемых для различения элементов некоторых множеств. По существу же источником двойственности является то обстоятельство, что одни и те же данные – результат решения одной задачи (более низкого уровня) и исходными данными другой задачи (более высокого уровня).

При медицинской диагностике необходимо решить ряд проблем. Это проблемы корректности вычислений при статистической зависимости признаков, недостаточность информации о распределении априорных вероятностей, неполнота и неоднородность информации, наличие «мешающих» факторов.

Другая группа проблем, свойственная задачам диагностики вообще, безотносительно к методам их решения и областям применения: большое количество признаков; различная информативность признаков; различная надежность измерений признаков.

Рассмотрим вопрос трансформации шкал, один из существенных аспектов которого – задача уменьшения количества признаков при сохранении приемлемого качества диагностики.

9.5.2 Сжатие и растяжение данных

Под сжатием данных будем подразумевать следующие два вида преобразований: замена вектора данных на вектор меньшей размерности; замена шкал значений компонентов вектора данных на более «грубые» шкалы того же вида либо на шкалы более низкого уровня. Растяжение данных есть процедура, обратная сжатию.

Специалисты в области теории сигналов могут увидеть в таком сжатии управление двумя группами характеристик: пространственно-временными и амплитудными.

Хорошо известный пример процедуры сжатия – дискретизация сигналов по времени: непрерывный процесс , удовлетворяющий условиям теоремы Котельникова, практически без потерь информации может быть заменен дискретным процессом , где  – шаг дискретизации по времени.

Другой пример – задача распознавания образов, где весьма остро стоит вопрос уменьшения количества признаков, позволяющего снизить вычислительные затраты ценой приемлемого снижения достоверности распознавания.

Еще один пример – задача визуализации данных, сводящаяся к проецированию данных из пространств большой размерности в пространства малой (1, 2, 3-мерное) размерности – эта задача известна как многомерное шкалирование.

Трактовка этих видов сжатия представителями «нефизических» наук - психологами, экономистами и др. - может быть иной: уменьшение размерности вектора данных есть сокращение перечня факторов, а замена шкал компонентов вектора - сокращение количества градаций, шкалы значений факторов.

В психологии и медицине не менее актуальна проблема как сокращения объемов исходных описаний объекта (знаки, симптомы, характеристики), так и формирования лаконичных, но достаточно полных, выходных описаний объекта (диагнозы, заключения специалистов).

Отметим кстати, что подход к задачам измерений с позиций теории шкал позволяет увидеть принципиальное сходство между данными «физического» и «нефизического» характера рис. 9.18. При этом первый вид сжатия соответствует направлению «по горизонтали», а второй – «по вертикали».

Эффективный и широко применяемый в психологии метод сжатия признакового пространства – факторный анализ, основная модель которого имеет вид системы равенств:

; ; .

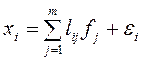То есть полагается, что значения каждого признака  могут быть выражены взвешенной суммой простых факторов , количество которых меньше числа исходных признаков, и остаточным членом  с дисперсией , действующей только на , который называют специфическим фактором.

Рис. 9.18 – Отображение различных данных